-


-
Chers utilisateurs du site maths-au-quotidien.fr,
Si vous souhaitez vous procurer l'ouvrage « Les maths au quotidien », vous pourrez le trouver ou le commander dans toute bonne librairie.
Vous avez aussi la possibilité de l'acheter directement via plusieurs sites marchands sur internet.
Bien à vous,
Les webmestres
-
Point info : une abeille c’est formidable.
Mais le fond choisi par les abeilles reste-t-il le moyen le plus économique pour la construction d’une alvéole ? En 1964, Fejes Toth a démontré que si le fond était formé de deux petits hexagones ainsi que de deux losanges, au lieu de trois rhombes, la quantité de cire serait, pour un même volume, inférieure de 0,35 % à ce qu’elle est avec les losanges. La différence est minime, pour une complexité du fond plus importante.
Les structures en nid d’abeille servent à augmenter la résistance d’un matériel, tout en garantissant une grande légèreté. La structure en nid d’abeille peut être constituée d’aluminium, de carton ou de plastique. Dans l’industrie des composites, l’âme d’un panneau sandwich est souvent constituée d’une structure en nid d’abeille sur laquelle sont apposées des plaques à base de résine et de fibre de verre. L’âme procure ainsi au panneau une résistance en compression plus importante, une plus grande capacité de déformation, ainsi qu’un taux de vide avoisinant les 95 %, permettant une légèreté du matériau. Ces structures sont employées en particulier dans l’industrie aéronautique, pour le remplissage de volumes creux, par exemple les extrémités des ailes, mais aussi dans l’automobile, le nautisme, l’éolien, les travaux publics. De tous les fonds rhombiques, c’est celui choisi par les abeilles qui est optimal :
De tous les fonds rhombiques, c’est celui choisi par les abeilles qui est optimal :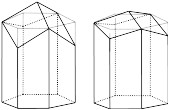
Voici deux alvéoles avec des fonds rhombiques différents :
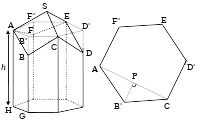
Quitte à changer d’unité de longueur, on peut considérer que la longueur du côté de l’hexagone AB’CD’EF’ vaut 1 unité de longueur (figure suivante). La longueur \(\scriptsize h = AH\) est plus grande que 1. L’inclinaison des losanges du fond par rapport aux parois latérales dépend de la position du point B sur l’arête de l’alvéole.
Posons donc \(\scriptsize x = BB’\).
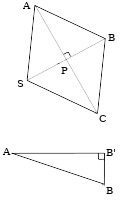
On va calculer l’aire du losange ABCS. Celle-ci est le produit des longueurs des deux diagonales divisé par 2.
Rappelons que P est le milieu de [AC]. (B’P) et (AC) sont perpendiculaires.
 Questions :
Questions :
1. Combien mesure, en degrés, l’angle \(\scriptsize \widehat{AB'P}\) ?
2. En déduire la longueur AP puis AC.
3. Calculer la longueur AB en fonction de \(\scriptsize x\).
4. Calculer la longueur BS.
5. Calculer l’aire du losange ABCS.
 6. Calculer l’aire du trapèze ABGH en fonction de \(\scriptsize x\) et de \(\scriptsize h\).
6. Calculer l’aire du trapèze ABGH en fonction de \(\scriptsize x\) et de \(\scriptsize h\).
7. Calculer l’aire de l’alvéole.
8. Étudier les variations de la fonction aire de l’alvéole A (fonction de \(\scriptsize x\)) et en déduire pour quelle valeur de \(\scriptsize x\) cette aire est minimale.
9. Calculer alors des mesures des angles du losange ABCS en degrés et minutes (un degré équivaut à 60 minutes).
Réponses :
Réponses détaillées dans l'ouvrage...
On a déjà remarqué qu’un fond rhombique assurait plus de solidité et un accolement parfait des deux feuilles d’alvéoles du gâteau de cire, mais ce fond utilise-t-il moins de cire qu’un fond plat hexagonal ? Eh bien OUI !!!
Question : Quelle est l’aire de l’alvéole si le fond est plat et hexagonal ?
Réponses :
Réponses détaillées dans l'ouvrage...
Point info : une abeille, c’est sympa.
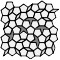 Cependant, on pourrait se demander si le pavage hexagonal, malgré ses atouts déjà vus plus haut, est le pavage du plan le plus économique. En effet, pour paver le plan, on peut accoler des polygones différents, qui ne sont pas forcément réguliers, ni même dont les côtés sont des segments.
Cependant, on pourrait se demander si le pavage hexagonal, malgré ses atouts déjà vus plus haut, est le pavage du plan le plus économique. En effet, pour paver le plan, on peut accoler des polygones différents, qui ne sont pas forcément réguliers, ni même dont les côtés sont des segments.
La réponse à cette question n’a été établie qu’en 1943, date à laquelle le mathématicien hongrois Fejes Toth démontra que la structure hexagonale régulière restait le polygone le plus économique pour paver le plan parmi tous les polygones à côtés droits.
Étant donné que les alvéoles sont construites avec de la cire chaude, on pourrait aussi se demander s’il n’y a pas moyen de minimiser encore la quantité de cire utilisée en construisant des côtés courbés. Fejes Toth pensait que la structure hexagonale régulière restait encore dans ce cas la plus économique, mais il n’a pas réussi à démontrer ce résultat. Ce n’est qu’en 1999 (eh oui, y’a pas très longtemps…) que Thomas Hales présente une longue preuve utilisant des mathématiques modernes démontrant que la structure hexagonale régulière reste effectivement la plus efficace.
De plus, un angle de 120° est peu fragile. Les coins carrés sont plus sensibles ; quant à ceux du triangle équilatéral, ils sont encore moins solides. Par ailleurs l’hexagone régulier est, de ces polygones, le plus « proche » du cercle, et sans doute le plus « confortable » pour les abeilles, à corps presque cylindrique, et pour leurs larves.Pourquoi des losanges pour fabriquer le fond de l’alvéole ?
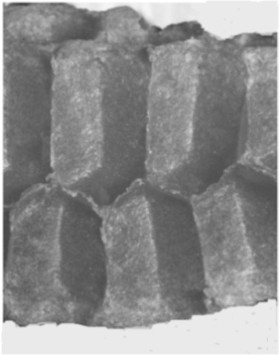 Le fond formé de trois losanges permet un adossement simple des alvéoles. Chaque fond d’alvéole d’une feuille du gâteau de cire vient s’imbriquer parfaitement entre les fonds de trois alvéoles de l’autre feuille. Le fait que les fonds se chevauchent parfaitement dans l’espace permet d’une part d’optimiser la place car il n’y a strictement aucune perte. D’autre part, cela permet de donner au gâteau de cire une structure beaucoup plus solide que si les fonds étaient plats. Voyons de plus près la solution choisie par les abeilles.
Le fond formé de trois losanges permet un adossement simple des alvéoles. Chaque fond d’alvéole d’une feuille du gâteau de cire vient s’imbriquer parfaitement entre les fonds de trois alvéoles de l’autre feuille. Le fait que les fonds se chevauchent parfaitement dans l’espace permet d’une part d’optimiser la place car il n’y a strictement aucune perte. D’autre part, cela permet de donner au gâteau de cire une structure beaucoup plus solide que si les fonds étaient plats. Voyons de plus près la solution choisie par les abeilles.
Point info : une abeille, c’est de toute beauté !
Les abeilles ont choisi un fond rhombique.
Que les abeilles choisissent un fond plat hexagonal ou bien un fond rhombique, cela donne le même volume à l’alvéole :
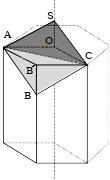
Considérons un tiers d’alvéole. On remplace le losange AB’CO qui constitue un tiers du fond hexagonal par le losange ABCS qui constitue un tiers du fond rhombique. En faisant cela, on ne change pas le volume du tiers d’alvéole car le volume ajouté, celui du tétraèdre OACS est égal au volume enlevé, celui du tétraèdre B’ACB. En effet, ces deux tétraèdres sont image l’un de l’autre par la symétrie centrale de centre P, P étant le centre du losange ABCS. Donc en choisissant un fond rhombique plutôt qu’un fond hexagonal, nos copines hyménoptères ne modifient pas le volume total de l’alvéole.Pourquoi une structure hexagonale pour les parois latérales de l’alvéole ?
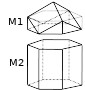
Découpons notre alvéole en deux morceaux que nous appellerons M1 et M2 comme sur le schéma ci-contre.
M2 est un prisme donc son aire latérale dépend de la forme de sa base (et de sa hauteur). Cette aire vaut alors (périmètre de la base)×hauteur. Intéressons-nous donc à la forme de la base de M2.
Il s’agit pour les abeilles de paver le plan pour pouvoir ensuite paver l’espace. L’abeille va choisir une même figure afin de faire des alvéoles identiques et dans un souci de simplicité et de symétrie, on s’attend à ce qu’elles choisissent un polygone régulier.
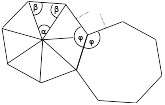 Questions :
Questions :
1. Pour un polygone régulier à n côtés (n ≥ 3), quelle est en fonction de n la mesure en degrés de l’angle \(\scriptsize \alpha\), de l’angle \(\scriptsize \beta\), de l’angle φ (angle entre deux côtés consécutifs) ?
2. Donner une condition nécessaire reliant k et n pour pouvoir accoler par un sommet k polygones réguliers à n côtés. Exprimer k en fonction de n.
3. Montrer que k est une fonction décroissante de n. Calculer k pour n = 3, 4, 5, 6, 7.
4. En déduire les polygones réguliers permettant de paver le plan avec un seul motif.
Réponses :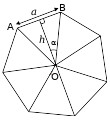
Réponses détaillées dans l'ouvrage...
On va maintenant exprimer le périmètre d’un polygone régulier à n côtés en fonction de son aire. Soit \(\scriptsize a\) la longueur du côté du polygone régulier à n côtés (figure ci-contre).
Questions :
1. Quel est le périmètre \(\scriptsize P\) de ce polygone ?
2. Donner l’aire du triangle AOB en fonction de \(\scriptsize h\) et a puis l’aire \(\scriptsize A\) du polygone. En déduire \(\scriptsize h\) en fonction de \(\scriptsize P\) et \(\scriptsize A\).
3. Écrire \(\scriptsize \alpha\) en fonction de n. Que vaut \(\scriptsize \tan \alpha\) ? En déduire \(\scriptsize h\) en fonction de \(\scriptsize a\) et n puis en fonction de \(\scriptsize P\) et n.
4. En déduire \(\scriptsize P\) en fonction de \(\scriptsize A\).
5. Maintenant, démontrer que, parmi le triangle équilatéral, le carré et l’hexagone régulier, pour une même surface, l’hexagone est le polygone régulier offrant le plus petit périmètre.
Réponses :
Réponses détaillées dans l'ouvrage...
Les abeilles ★ ★ ★ ★ ★

 Tout quidam que nous sommes sait que les alvéoles des ruches d’abeilles ont une ouverture de forme hexagonale. Les abeilles forment leur gâteau de cire en accolant deux feuilles d’alvéoles comme sur la photo ci-contre :
Tout quidam que nous sommes sait que les alvéoles des ruches d’abeilles ont une ouverture de forme hexagonale. Les abeilles forment leur gâteau de cire en accolant deux feuilles d’alvéoles comme sur la photo ci-contre :
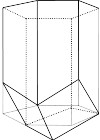
Une alvéole pourrait être un prisme, c’est-à-dire que le fond de l’alvéole pourrait être également un hexagone régulier, sauf qu’en réalité, celui-ci n’est pas plan mais est composé de l’accolement de trois losanges (un synonyme de losange est rhombe pour les savants) identiques comme sur le schéma ci-contre :
Chaque losange constitue un tiers du fond d’une alvéole voisine.
Le bord d’entrée de l’alvéole ainsi qu’une bonne partie de la section de celle-ci par un plan parallèle à ce bord est très précisément un hexagone régulier dont le côté mesure environ 3 mm. La profondeur de l’alvéole est de 11,5 mm environ.
La forme hexagonale des alvéoles fut observée par Aristote au IVe siècle av. J.-C., dans son « Histoire des Animaux », puis étudiée géométriquement au IVe siècle apr. J.-C. par le mathématicien grec Pappus, qui proposa déjà que cette structure hexagonale soit choisie par les abeilles dans un souci d’économie.Ce n’est qu’au XVIIIe siècle que la forme rhomboïdale du fond fut remarquée. G. F. Maraldi, astronome à l’Observatoire de Paris, mesura en 1712 les angles de ces losanges, égaux à environ 109°28’ et 70°32’.
Intéressé par la forme de ces alvéoles, le physicien Réaumur pressent comme Pappus que les abeilles bâtissent leur gâteau de cire en optimisant la quantité de cire utilisée. Pour vérifier cela, il demanda au géomètre allemand Köenig de déterminer quelle était la cellule à entrée hexagonale et à fond composé de trois losanges identiques, qui pouvait être construite avec le moins de cire possible. Par calcul différentiel, Köenig trouva en 1739 que les angles de ces losanges devaient être égaux à 109°26’ et 70°34’. Mais en 1743, le mathématicien écossais Maclaurin montra que Köenig avait commis une erreur dans ses calculs, et que les angles des losanges minimisant la surface du fond des alvéoles étaient exactement ceux indiqués par Maraldi : 109°28’ et 70°32’ !!! C’est ce que vous allez vous-même retrouver plus loin.
Remarque : de part les dimensions constantes et précises des alvéoles d’abeilles, Réaumur a proposé l’idée novatrice de prendre le côté d’une alvéole comme la référence d’un système de mesures invariables, telle que l’est aujourd’hui le mètre.
Miroir, mon beau miroir ★ ★ ★ ☆ ☆
Vous voulez équiper votre salle de bain d’un miroir sympa afin de pouvoir vous regarder entièrement dedans. Dans un souci de place et/ou de prix, vous voulez acheter un miroir ayant une hauteur minimale et satisfaisant à vos exigences.
Vous mesurez le recul que vous avez dans votre salle de bain : 2 mètres...
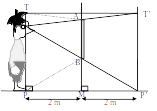 La figure ci-contre vous représente dans votre salle de bain, à 2 mètres du miroir avec OP = 1,58 m (distance de votre œil au sol) et TP = 1,70 m (c’est votre taille).
La figure ci-contre vous représente dans votre salle de bain, à 2 mètres du miroir avec OP = 1,58 m (distance de votre œil au sol) et TP = 1,70 m (c’est votre taille).
T’ est le symétrique de T et P’ est le symétrique de P par rapport à la droite (AB).
Questions :
1. Quelle est la distance AB (taille minimale du miroir) ?
2. À quelle hauteur le miroir se trouve-t-il, c’est-à-dire quelle est la distance AM ?
3. Quelle curiosité se dégage des calculs précédents ?
Réponses :
1. Dans le triangle OPP’, la droite (AB) est parallèle au côté [OP] et passe par le milieu du côté [PP’]. D’après la réciproque du théorème des milieux, la droite (AB) coupe le côté [OP’] en son milieu. Donc B est le milieu de [OP’].
Dans le triangle OT’P’, la droite (AB) coupe le côté [OP’] en son milieu et est parallèle au côté [T’P’]. D’après le théorème des milieux :
AB = \(\scriptsize \frac{T'P}{2} = \frac{1,7}{2}\) = 0,85 m
2. Calculons la distance AM :
D’après le théorème des milieux :
BM = \(\scriptsize \frac{OP}{2} = \frac{1,58}{2} \) = 0,79 m
On en déduit la hauteur à laquelle le haut du miroir doit se situer :
AM = AB + BM
AM = 0,79 + 0,85 = 1,64 m
Le haut du miroir doit se trouver à 1,64 m du sol.
3. Les calculs précédents montrent que la distance de recul par rapport au miroir n’intervient pas dans le fait de se voir entièrement. Autrement dit, quelle que soit la distance à laquelle on se place du miroir, on se verra toujours entièrement. Par contre les détails changeront. Il vaut mieux être à une certaine distance pour s’admirer dans son costard tout neuf, et près du miroir pour se percer ses boutons d’acné sur le front…
Quelques extraits...
Miroir, mon beau miroir (collège)
Les abeilles (lycée)
Histoire du mètre p.284
Informatique et nombres binaires p.287
Règle logarithmique p.289Un petit mot sur les nombres complexes
THÈMES
Le nombre d’or
Le nombre d’or p.295
Le rectangle d’or p.295
La reproduction des abeilles p.296
Botanique p.298
Architecture p.299
Peinture p.301
La spirale d’or p.302Les fractales
Acoustique p.306
Bourse p.306
Maçonnerie p.306
Nature p.307Les coniques
La parabole p.311
Four solaire p.311
Fluide p.312
Astronomie p.312
Les optiques de phares de voitures p.313Télécommunications p.313
Ponts p.313
L’hyperbole p.314
Navigation p.315
Astronomie p.315
Centrale nucléaire p.316
L’ellipse p.317
Acoustique p.317
Astronomie p.318
Architecture p.318
Jardinerie p.318Chaînette
Haute tension p.320
Architecture p.322
Transport p.324Les solides de Platon
Chimie p.325
Minéralogie p.325
Football p.327
Dés à jouer p.328
Génétique p.328Remerciements
Crédits photographiques
Index
Calculer simplement l’aire d’une pièce ou d’un terrain p.138
La cuve p.140Météo
Amplitudes thermiques p.145
Connaître la distance qui sépare de la foudre p.145
Température p.147
Chanter sous la pluie p.147
C’est hot p.153
Comme un ouragan p.156Modèles économiques
Indices boursiers p.157
Le surbooking p.157
Volatilité p.159
Coût de production p.159
Indice de Gini p.162
Offre et demande p.166Musique-Acoustique
La gamme de Pythagore p.173
De bonnes vibrations p.174
Des fractions haut de gamme p.175
La gamme de Zarlino p.176
La gamme tempérée p.177
Harmoniques p.179
Composition p.180
J’ai la guitare qui me démange p.183Acoustique p.183
Compact disc p.184Navigation
Bateaux tamponneurs p.185
Gardons le cap p.187
Remorquer un bateau p.188
Le radar p.188
Avion de ligne p.190Porte-monnaie
Cinéma en famille p.191
Salaire de l’heure p.191
Nos amies les caissières p.191
Pendant les courses p.192
Variétés de fruits p.192
Pouvoir d’achat p.193
Les soldes p.194
Au marché p.194
Comparer des offres p.194
TVA p.195
Opérateur internet p.196
Les salaires p.197
Économiser l’eau p.198
Location p.200
Optimisation p.200
Impôts p.201Repérage
Retrouver facilement le sud p.205
Jeu d’échec p.205
Un trésor p.206Repérage sur la sphère p.207
Tour de magie p.210
Se repérer dans certaines grandes villes p.211
S’orienter en randonnée p.213Représentations visuelles
Format de feuille p.215
La perspective cavalière p.215
Le pantographe p.218
Peinture p.220
Images de synthèse p.225
Courbes de Bézier p.227
Colorier une carte p.227Santé
Numéro de sécurité sociale p.229
Aux urgences p.230
La mucoviscidose p.231
La scintigraphie p.235Société
Au feu, les pompiers p.239
Élection présidentielle p.240
Jurés aux États-Unis p.241
Loi de Benford p.243
Couleur café p.245Sport
Foot p.249
Replacement au tennis p.249Prêts pour les jeux p.252
Rugby p.253
À Roland Garros p.254
Golf in the Moon p.255
Club de vacances sportif p.257
Tournoi de foot p.258Transports
Au parking p.261
Angle mort p.261
Sécurité routière p.263
Le géomètre p.263
Réglage des feux de croisements d’une voiture p.264
Synchronisation des p.feux
tricolores p.265
Synchronisation des feux (partie II p.267
Distance d’arrêt p.269
Tunnel de Samos p.271
Temps de parcours p.272
Courbes de Bézier p.272
Ça vaut une plaque p.277
Fais ta valise p.278
Virages p.279Unités
Les unités de mesures anglo-saxonnes p.283
Le temps p.283Introduction
Animaux
L’araignée meurtrière p.7
Toutous et matous p.9
Cigales périodiques p.11
Les abeilles p.12
Le pelage des animaux p.18Astronomie
Éclipse totale de Soleil p.19
Calculer le rayon de la Terre p.20
Aérospatiale p.21
Écriture scientifique p.22
Magnitude des étoiles p.23
Magnitude d’un séisme p.25
Mouvement de la Lune p.25Banque
Relevé bancaire p.27
Numéro de compte bancaire p.27
Taux bancaires p.28
Taux bancaires (II) p.30
Plan de remboursement p.31
Payer content ou emprunter p.33Bricolage
La corde à treize nœuds p.35
Ça passe ou ça casse p.35Pot de peinture p.36
Pose de carrelage mural p.37
Dallage en maçonnerie p.37
Pavages p.38
Pose de carrelage p.44
Rempotage p.47
Miroir, mon beau miroir p.48
Coin d’une pièce p.49
Arroser ses pieds de tomates p.49
C’est bancal p.50
La barre de « faire » p.50
Secrétaire à la maison p.51Codages
Code barres p.53
Cryptographie p.54Cuisine
La recette de cuisine p.63
La recette de cuisine (épisode II) p.64
Appétit gargantuesque p.64
Pizzas p.65
Problème pour peser des aliments p.65
Thermostat de four... p.66
Partager un gâteau en parts égales p.67
Temps de cuisson p.69
Les melons p.70Cueillette de girolles p.71
Des pizzas, encore des pizzas … p.72
Équilibre alimentaire p.74
Boite de conserve p.76
Une application qui va vous refroidir... p.81
Il faut maintenant partager le gâteau p.83
Un baba cool p.83Dates et heures
Attendant l’an 2000 p.87
Calendrier p.87
Aiguilles p.88
Datation au carbone 14 p.89Dynamique de populations
Une population de levures p.93
Proie-prédateur p.98
Recensement p.100
Classes d’âge p.101Insolite
Terre encordée p.103
Le monde de Némo p.104
Tour de taille p.105
Paul le poulpe p.105
Dates d’anniversaire p.106
Naissances p.109
C’est dans la boite p.110Loisirs
Jeu télévisé p.111
Sur les bords de Loire p.112
Alerte à Malibu p.113
À la pêche p.114
J’ai les boules p.115
Plongée p.118
100 % des perdants ont tenté leur chance p.119
Attention chien méchant p.122
Les tours de Hanoï p.122
Un jeu de NIM p.124
Comme sur des roulettes p.125
Les joies du camping p.129
Les 11 merveilles du Moude p.130
Organisation d’associations p.132Maison
Terrain constructible p.133
Profondeur d’un puits p.133
La table à repasser p.134
Écran plasma p.134
Calculer la hauteur d’une maison p.135
Hauteur d’un immeuble p.136
Mesurer la hauteur d’un édifice p.136
Table des matières
Enfin, les parents d’élèves, les étudiants, le grand public, et tous ceux qui aiment les mathématiques, trouveront intérêt à cet ouvrage.
Dans ce livre, utilisable par tous, nous vous présentons une série d’exercices, de points informatifs, au plus près possible des programmes scolaires et de la vie courante. Les exercices couvrent une très large partie des programmes du secondaire.
Nous avons eu en contact un certain nombre d’interlocuteurs dans différents corps de métiers, afin d’essayer d’être au plus près de la réalité, dans notre contenu.
Une partie des articles a été rédigée à partir d’informations glanées dans les manuels du secondaire, et à partir d’informations sur une multitude de sites internet sans lesquels ce livre n’aurait pu voir le jour.
Nous avons volontairement limité les applications à la physique et les applications des statistiques, dont personne ne conteste l’utilité…
Nous prions les lecteurs les plus rigoureux de nous excuser des abus qu’ils trouveront dans quelques réponses. Nous avons opté parfois pour la concision dans la rédaction plutôt que dans la rigueur parfaite.
Les articles purement informatifs (hormis les thèmes), n’utilisant pas la contribution du lecteur, seront sur fond gris.
En regard des notions qu’il comporte, chaque exercice est doté de une à cinq étoiles, relatives au niveau de difficulté de l’exercice :
★ ☆ ☆ ☆ ☆ : très facile
★ ★ ☆ ☆ ☆ : facile
★ ★ ★ ☆ ☆ : moyen
★ ★ ★ ★ ☆ : difficile
★ ★ ★ ★ ★ : très difficile
Nous développons un site internet dédié à ce livre et en complément de celui-ci. Il se trouve à l’adresse suivante : https://maths-au-quotidien.fr.
Sur ce site figurent :
- des exercices interactifs évalués : INTERACT.
- des TP téléchargeables pouvant être faits en classe : TP .
- des animations : ANIM.
- des devoirs en temps libre : DM.
- des documents utilisant l’algorithmique : ALGO.
- d’autres ressources mathématiques : TABLEUR…
Toutes ces ressources sont associées à des situations concrètes, dont quelques-unes issues de cet ouvrage.
Les exercices de cet ouvrage en lien avec un ou plusieurs documents du site seront estampillés des logos précédents.
Belle lecture à tous et belles mathématiques…
Les auteurs.Il pourrait, par exemple, se limiter à un cadre purement scolaire : « Les mathématiques ne me servent qu’à obtenir mon brevet et mon bac… ». Avec une vision plus alarmiste, ceci pourrait être une des causes de sa démotivation de l’apprentissage des mathématiques. Dès lors, comment certains élèves expriment-ils cette frustration, cette vision dévalorisante d’un enseignement aussi important ? Eh bien, par exemple, en interpellant un(e) enseignant(e) durant son cours : « Mais monsieur (madame), à quoi ça sert !? ».
Les applications des mathématiques, quand bien même elles sont présentées aux étudiants, ne sont vues qu’à haut niveau d’études, de manière éparse. C’est la raison pour laquelle même un professeur de mathématiques a du mal à répondre de manière claire et concise à la question précédente.
Tout d’abord, un des intérêts des mathématiques est qu’elles sont, comme d’autres disciplines (histoire-géographie…) un objet de connaissances. Avant leur aspect utilitaire, on peut par conséquent les considérer sous une perspective culturelle. Les mathématiques ont en particulier leur place dans l’histoire des hommes et de la pensée humaine.
Ensuite, une utilité majeure des mathématiques dans le secondaire est d’éduquer le raisonnement. Au travers d’une unité cohérente, l’élève apprend à faire des déductions, à utiliser des règles de logique, à vérifier, à conjecturer, à démontrer. En ce sens, les mathématiques sont une méthodologie de l’esprit, apprenant, d’une certaine manière, à mieux raisonner.
D’un point de vue pratique, les mathématiques apprennent donc à mieux analyser, trier, synthétiser la multitude d’informations qui proviennent du monde extérieur et notamment les informations chiffrées.
Durant un cours, une séance d’exercices, ou un devoir à la maison, il n’est pas anormal qu’un élève s’interroge sur l’utilité de ce sur quoi il est évalué. Apprendre les notions de base des mathématiques comme le calcul mental, la découverte des différents ensembles de nombres (entiers, décimaux, relatifs, rationnels…), la géométrie, est une chose dont un élève peut facilement se donner une idée de l’utilité dans la vie quotidienne. Mais des notions plus sophistiquées, étudiées dès le collège, comme les fonctions linéaires, l’arithmétique, le théorème de Thalès, le théorème de Pythagore, entre autres, entrent dans un cadre où les élèves ont du mal à se faire une représentation dans la vie courante.
Un élève ayant des doutes sur l’utilité de la notion qu’il est en train d’apprendre peut, en feuilletant quelques uns de nos articles se rapportant à la notion en question, se donner une vision plus globale, sortir un court instant du cadre scolaire qui lui est imposé et se projeter dans des situations concrètes et les appliquer lui-même. Voilà une façon de donner un sens concret aux notions qu’il apprend tout au long de sa scolarité et par la même occasion de stimuler sa curiosité et sa motivation.
Un enseignant peut apporter des illustrations concrètes, en accord avec les programmes en vigueur, des notions qu’il aborde durant ses cours. Ces illustrations seront au plus proche de ce qui entoure les élèves dans la vie quotidienne ou dans les différents métiers qu’ils envisagent de faire. Il peut en outre apporter des compléments ou des extensions, toujours concrets, en réutilisant les différents thèmes de cet ouvrage (fractales, coniques…).
Introduction
Mais à quoi servent les mathématiques ? En voilà une question ! Celle-ci est familière pour nous bien sûr, professeurs, dans la bouche de nos élèves, mais peut-être aussi pour vous, lecteurs, qui maintenant avez ce livre entre vos mains.
Les mathématiques possèdent de très nombreuses applications dans le monde qui nous entoure. Elles nous aident à améliorer notre quotidien sans que la plupart d’entre nous ne s’en rendent compte. On les retrouve dans la nature, dans l’industrie, dans divers métiers, dans les nouvelles technologies…
Les mathématiques sont le langage de la physique, discipline prestigieuse tentant de décrire et de mesurer le monde. La physique est l’impératrice des mathématiques appliquées, où les grandeurs du monde sont mises en relations par des équations, où la dérivée et l’intégration sont reines.
« Le grand livre de la nature était écrit dans la langue des droites, des cercles, la langue de la géométrie et des mathématiques ».
« Les mathématiques sont le langage de l’Univers » Galilée (1564-1642).
Les sciences naturelles, les sciences économiques, utilisent largement les outils mathématiques, comme les fonctions, la notion de dérivée, d’intégrale, les statistiques, les probabilités…
L’informatique est nombres, logique et algorithmes.
Sans mathématiques, il n’y a pas de technologie possible. Il y a des mathématiques cachées partout autour de vous, dans votre télévision, dans votre téléphone portable, dans vos placards de cuisine… et vous aurez beau y mettre des boules anti-mathématiques, vous ne vous en débarrasserez pas.
Les mathématiques sont indissociables de la philosophie. La plupart des philosophes historiques étaient des savants ou avaient de bonnes connaissances mathématiques : Platon, Aristote, Descartes, Pascal, Spinoza, Leibniz, Kant, Bachelard…
« Les mathématiciens ont autant besoin d’être philosophes que les philosophes, mathématiciens » Leibniz (1646-1716).
Il y a également une forte notion d’esthétisme et de finesse dans les mathématiques. En dehors d’énoncer des règles de perspectives qui permettent la représentation du monde et donc des jugements esthétiques, on trouve par exemple dans les mathématiques de « jolies démonstrations » ou bien de « forts beaux raisonnements ». Il s’agit réellement d’un ressenti esthétique, comme la vision d’un paysage mirifique.
« Une théorie est bonne lorsqu’elle est belle » Henri Poincaré (1854-1912).
Dans le secondaire, les mathématiques sont présentées comme une matière possédant un certain degré d’importance, du point de vue du volume horaire et des coefficients. La motivation de l’élève est un facteur primordial pour sa réussite scolaire. Pour certaines personnes, par rapport à d’autres disciplines moins abstraites, la question de l’intérêt des mathématiques se pose davantage. Un élève peut être aussi amené à s’interroger sur l’utilité de ce qu’il apprend, en regard de sa profession future. S’il ne trouve aucun lien, ou si aucune réponse ne lui est apportée, l’élève peut alors plonger dans une vision très étriquée de l’utilité de ce qu’il apprend.

Les auteurs
Matthieu Colonval et Abdelatif Roumadni -

Les maths au quotidien
Les maths au quotidien est initialement un ouvrage recoupant un ensemble d'exercices et d'articles issus de la vie courante dans des domaines très variés.
Les auteurs, Matthieu Colonval et Abdelatif Roumadni, vous proposent sur maths-au-quotidien.fr une extension et un complément de l'ouvrage avec, entre autres, des activités interactives évaluées, des extraits de brevet et de baccalauréat, des exercices exploitables en classe... -
Attention : pour feuilleter quelque pages, vous devez installer le plugin flashplayer.