Comment Google classe ses pages web ?

Niveau : terminale générale, Maths Expertes.

Lien avec Les Maths au quotidien : Navigation.

Exercice

Lorsqu’un internaute cherche des informations sur Internet, il tape un ou plusieurs mots-clés sur un moteur de recherche, comme par exemple Google. Celui-ci fonctionne en deux temps : d'abord, il répertorie les pages qui correspondent au(x) mot(s)-clé(s) entré(s), puis il hiérarchise ces pages web selon leur intérêt.

D’accord, mais comment définir « objectivement » l’intérêt d’une page web ?
Google a fait la sensation en 1998 en donnant une définition de ce qu’est l’« importance » d'une page web : le PageRank de la page, dont nous allons étudier le principe.

L’idée est née lors de la thèse de doctorat des deux fondateurs de Google, Sergey Brin et Lawrence Page, qui ont mis au point un algorithme itératif « simple », basé essentiellement sur la résolution d’un système d’équations linéaires.

La hiérarchisation des pages web qui en découle a fait le succès de Google et la fortune de ses fondateurs, car elle correspond aux attentes des utilisateurs.

Le principe fondamental sur lequel repose cet algorithme est l’utilisation du nombre de liens hypertexte contenues dans les différentes pages web de l’internet, et qui permettent de naviguer d’une page vers une autre.

Dans ce document, on écrira \(i \rightarrow j\) si la page \(i\) pointe vers la page \(j\). Par conséquent, on peut donc considérer le web comme un immense graphe, dont chaque page web i est un sommet et chaque lien \(i \rightarrow j\) est une arête.

Soit \(m\) le nombre de pages web correspondant à un (des) mot(s)-clé(s) entré(s) par l’utilisateur.
On numérote les pages par \(1, 2, 3, …, m\). Ainsi chaque page \(i\) émet un certain nombre \(l_i\) de liens vers des pages « voisines ». À noter que les arêtes sont orientées : si l’on a \(i \rightarrow j\), on n’a pas forcément le sens inverse \(j \rightarrow i\).

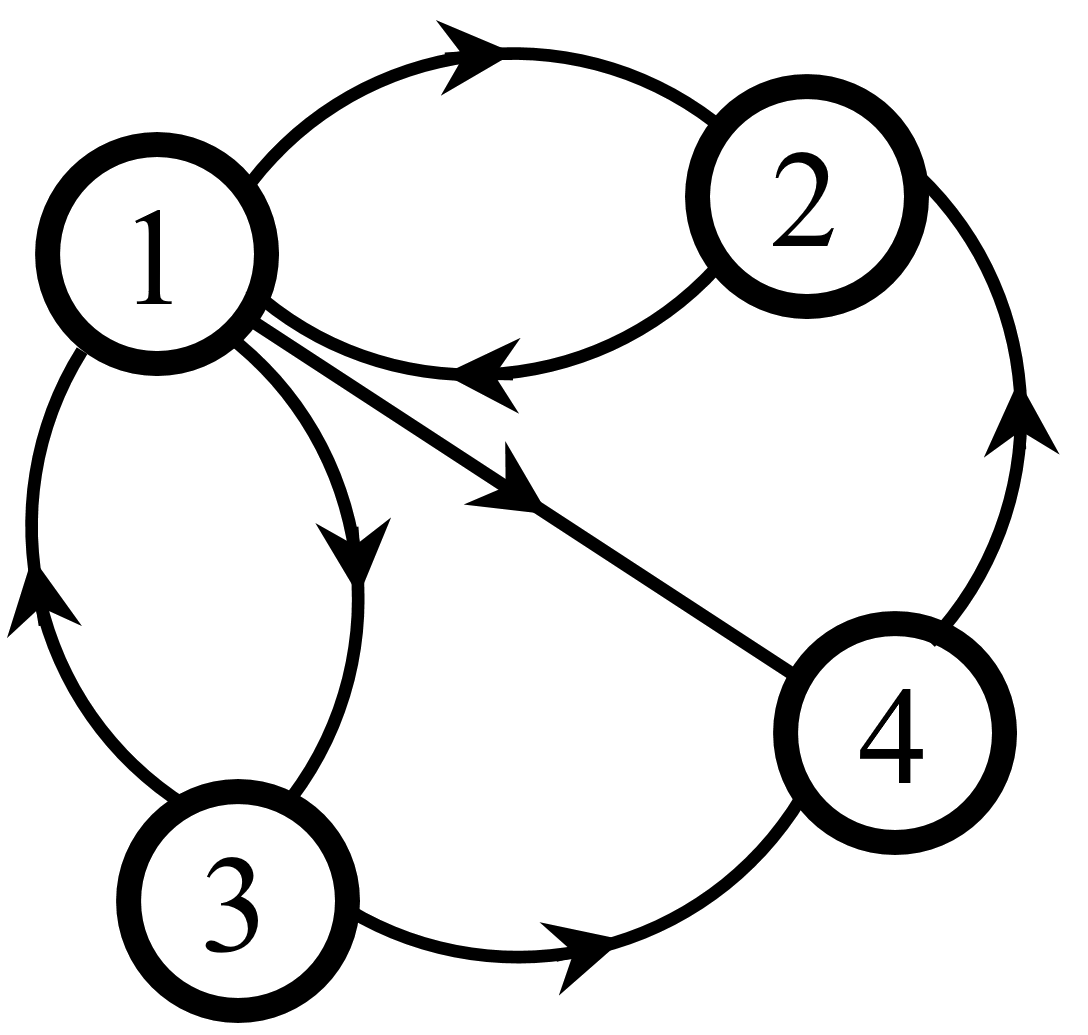
Par exemple, voici un « mini web », constitué de 4 pages web :

Dans cet exemple, \(m\) est égal à 4.
On a les liens \(1 \rightarrow 2, 2 \rightarrow 1, 1 \rightarrow 3, 3 \rightarrow 1, 1 \rightarrow 4, 3 \rightarrow 4, 4 \rightarrow 2\).
\(l_1 = 3,\, l_2 = 1,\, l_3 = 2,\, l_4 = 1\).


L’idée est d’associer à chaque page \(j\) une mesure d’importance \(u_j\), que l’on va appeler la pertinence de la page. On souhaite que cette mesure soit un nombre réel positif ou nul, avec la convention que plus \(u_j\) est grand, plus la page \(j\) est « importante ».

Le principe est le suivant :

Pour commencer, il est clair que la pertinence d’une page web est liée au nombre de liens qui mènent à cette page. Une première idée pourrait être alors que la pertinence d'une page corresponde au nombre de liens qui mènent à elle.

Mais cette idée souffre de deux faiblesses :

• Elle place tous les liens à égalité alors qu’une page « importante » qui pointe vers ma page doit donner plus d’importance à ma page qu’une page moins importante…
  
• Une personne qui voudrait donner arbitrairement beaucoup d'importance à sa page web pourrait se créer un petit panel d’autres pages qui pointeraient toutes vers celle-ci…
  5 / 15

D’autre part, si une page émet beaucoup de liens, on peut considérer quelque part qu’elle ne sait pas faire de choix. Ses liens seront donc moins importants que si elle en émettait peu. Si cette page pointe vers la mienne, pour le calcul de la pertinence de ma page web, la prise en compte de la pertinence de cette page (qui peut être faible ou élevée…) doit alors être pondérée par le nombre de liens sortant de celle-ci.

Finalement, pour \(j\in{1, 2, …, m}\), la pertinence \(u_j\) de la page web \(j\) est définie comme suit : $$u_j = \sum_{i \rightarrow j } \frac{u_i}{l_i}$$ les \(u_i\) désignent les pertinences des pages web pointant vers la page \(j\) et les \(l_i\) désignent les nombres de liens de ces mêmes pages.

La somme compte chaque lien reçu par la page \(i\) avec poids \(\frac{u_i}{l_i}\). Ceci tient compte favorablement de la pertinence \(u_i\) de la page \(i\), et défavorablement du nombre \(l_i\) des liens qui en sont émis.
Ces \(m\) équations forment un système linéaire (à \(m\) inconnues) que l’on va écrire matriciellement :
Pour tout couple d’indices \(i, j\in{1, 2, \ldots, m}\), on définit le nombre $$Aij = \left\lbrace \begin{array}{1} \frac{1}{l_i} \text{ si } \rightarrow j \\ 0 \text{ sinon }\end{array} \right\rbrace $$ On obtient ainsi une matrice \(A = (A_{ij})\), et notre équation s’écrit sous formematricielle comme \(X = XA\), avec \(X\) la matrice ligne \((u_1 \, u_2 \, … \, u_m)\). Les coefficients de la matrice \(X\) sont les pertinences de chacune des pages \(1, 2, …, m\). Dans la matrice \(A\) précédente, on peut remarquer la propriété suivante des coefficients \(A_{ij}\) : la somme des coefficients de chaque ligne vaut 1. En effet, pour tout \(i\in{1, …, m}\), $$\sum_{j=1}^{j=m}A_{ij}=\frac{1}{l_i}+\frac{1}{l_i}+ … +\frac{1}{l_i}=\frac{l_i}{l_i}= 1$$ \(l_i\) termes car il y a \(l_i\) liens de la page \(i\) vers la page \(j\).

Les coefficients \(A_{ij}\) (tous positifs ou nuls) peuvent donc s’interpréter comme la probabilité, pour un « surfeur aléatoire » qui se trouverait à la page \(i\), de suivre « au hasard » le lien qui l’amènerait à la page \(j\). Tous les liens de la page \(i\) sont équiprobables. Cette probabilitées \(t\) donc définie de la manière suivante : si \(l_i\) liens sont issus de la page \(i\), la probabilité pour que le surfeur aléatoire passe de la page \(i\) à une des pages vers lesquelles elle pointe est \(\frac{1}{l_i}\) , la probabilité pour qu’il se dirige vers une autre est 0.
Notons \(X_n\) la variable aléatoire indiquant la position (numéro de page) du surfeur aléatoire après \(n\) clics. On a vu que le nombre \(A_{ij}\) est la probabilité de se retrouver en un clic sur la page \(j\) sachant qu’on est sur la page \(i\). De manière plus mathématique, cela s’écrit $$\large A_{ij} = P_{(X_n=i)}(X_{n+1} = j)$$

De plus, après \(n\) clics, le surfeur est soit sur la page 1, soit sur la page 2,… soit sur la page \(m\) et ne peut être sur deux page en même temps : les \(m\) évènements \({X_n = 1}, {X_n = 2}, …, {X_n = m}\) forment donc une partition.
Par la formule des probabilités totales, on a : $$\large P(X_{n+1} = j) =\sum_{i=1}^{i=m} P_{(X_n =i)}(X_{n+1} = j) \times P (X_{n} = i) =\sum_{i=1}^{i=m} A_{ij} × P (X_{n} = i)$$ En notant \(U_n\) la matrice ligne \((P(X_n = 1) \, P(X_n = 2) \, … \, P(X_n = m))\), les relations précédentes peuvent se traduire par la relation matricielle suivante : $$U_{n+1} = U_nA$$

Si toutes les pages web communiquent, on montre que la matrice \(Un\) a pour limite la matrice \(X\) quand \(n\) tend vers \(+\infty\), dans le sens où \(P(X_n = 1)\) converge vers la pertinence \(u_1\), \(P(X_n = 2)\) converge vers la pertinence \(u_2, …, P(X_n = m)\) converge vers la pertinence \(u_m\).

La pertinence d’une page s’interprète donc comme la probabilité de se retrouver sur cette page après un très grand nombre de clics…

Un surfeur imaginaire qui parcourt indéfiniment Internet passera plus de temps sur les pages « importantes » et moins sur les autres, proportionnellement à la pertinence de la page.

En réalité, il existe beaucoup de pages web qui ne possèdent pas de lien hypertexte. Par conséquent si l’on considère qu’un internaute change de page seulement par lien hypertexte, et si celui-ci arrive sur l’une de ces pages, il se retrouvera bloqué. De manière plus subtile, il peut aussi arriver que l’internaute soit bloqué dans une portion du web, sans pouvoir s'y échapper. De plus, chacun sait que l’on peut choisir à tout moment une autre page donnée par le moteur de recherche et ceci sans suivre de lien donné.
C’est pourquoi Google utilise un modèle plus raffiné, et l’internaute a la possibilité de s’échapper et de revenir sur l’une quelconque des pages qui traitent son sujet.

Reprenons notre exemple précédent, mais en introduisant un paramètre \(c\in [0 ; 1]\), appelé coefficient d’échappement :

• avec probabilité \(c\), le surfeur abandonne la page actuelle et recommence sur l’une des \(m\) pages du web, choisie de manière équiprobable (il peut rester sur la page actuelle…).
• avec probabilité \(1 - c\), le surfeur suit un des liens de la page actuelle \(i\), choisi de manière équiprobable parmi tous les liens proposés par cette page.

Remarque : la valeur \(\frac{1}{c}\) est le nombre moyen de pages visitées avant de recommencer aléatoirement sur une page.

Comme les concepteurs de Google, on va prendre \(c = 0,15\), ce qui correspond à suivre environ 6 liens en moyenne.

Encore une fois, on étudie la position du surfeur au bout de \(n\) clics.
Pour cela, on note à nouveau \(X_n\) la variable aléatoire indiquant le numéro de la page web consultée par le surfeur aléatoire après \(n\) clics. \(A\) est la même matrice qu’avant, donnant les probabilités de passage d’une page à une autre en suivant un lien et on note à nouveau \(U_n\) le vecteur ligne \((P(X_n = 1)P(X_n = 2)…P(X_n = m))\).

On note \(C\) la matrice ligne dont tous les coefficients sont égaux à \(\frac{1}{m}\) .

On montre alors :

• que la suite de matrice ligne \((U_n)\) vérifie la relation \(U_{n+1} = U_n(0,85A) + 0,15C\).
• qu’il existe une et une seule matrice ligne \(L\) telle que \(L = L(0,85A) + 0,15C\).
• que notre suite \((U_n)\) converge vers la matrice \(L\).

Les pertinences des pages \(1, 2, 3, … m\) sont données par les coefficients respectifs de la matrice ligne \(L\).

Remarques :

• La suite itérative \((U_n)\) converge toujours vers \(L\), indépendamment de la position initiale \(U_0\). Or, Google est amené à rafraichir ses données régulièrement (une fois par mois ??), car le web évolue sans arrêt. Pour ce calcul, il est probable que Google choisisse pour le nouveau \(U_0\) la matrice de pertinences \(L\) du mois précédent. Ainsi, la convergence vers \(L\) se fera plus rapidement et moins d’itérations seront nécessaires pour réajuster \(L\).
  
• En réalité, la matrice \(A\) représentant le web est gigantesque ; cependant la plupart de ses coefficients sont égaux à zéro puisque qu’une page n’émet généralement qu’un nombre modeste de liens. On dit qu’une telle matrice est une matrice creuse. Cela réduit considérablement les calculs, même si ceux-ci restent faramineux.

Pour finir :
Notons bien que ce document explique le principe du calcul de pertinence d’une page web. Cependant la formule exacte donnant le PageRank de Google est toujours secrète. Il semblerait que ce PageRank soit liée à la pertinence d’une page web par une échelle logarithmique...

De nos jours, un certain nombre d'autres éléments sont utilisés pour classer les pages web, par exemple l'ancienneté du nom de domaine, la présence de mots-clés dans ce nom de domaine ou bien la localisation du serveur web...