Filtrage bayésien du spam
Niveau : terminales
Lien avec le programme : probabilités conditionnelles, indépendance, algorithmique, exponentielle et logarithme népérien.
Lien avec Les maths au quotidien : Navigation (sur internet).
Exercice en lien avec une autre discipline en voie générale (ISN).
Document annexe : Ressource ISN « Le filtrage du spam »
(Note : la formule \(\sum_{mot\in ligne} P_{mot}(M).score(mot)\) utilisée dans le document est artificielle).

1 / 45

2 / 45
Partie I- Introduction
Lorsque nous recevons du courrier électronique dans notre boite mails, un grand nombre de messages sont
indésirables ;
ce sont les spams, appelés pourriels en français.
Depuis la fin des années 1990 sont apparus des méthodes et logiciels anti-spam, capables de traiter efficacement le tri
des messages en fonction de « courriel légitime » et « spam ».
La réception d’une grande quantité de spams (près de 90 % de notre courrier en moyenne selon certaines sources) peut avoir
un impact important en termes de coût pour une entreprise ; au niveau mondial, les entreprises dépenseraient jusqu’à 20
milliards de dollars par an pour lutter contre les courriers électroniques non sollicités, les communications en ligne
indésirables et le hameçonnage associés.
L’une des composantes essentielles du traitement anti-spam du courriel repose sur un filtre probabiliste :
le
filtre bayésien (du nom de Thomas Bayes, mathématicien et pasteur britannique, connu pour la formule éponyme en probabilités).
Un filtre bayésien est présent dans la très grande majorité des logiciels anti-spam.
Nous allons par la suite étudier le principe du filtre bayésien dit naïf. Un article faisant référence en la matière est celui
de Paul Graham :
A Plan for Spam (suivi de
Better Bayesian Filtering).
3 / 45
Certains mots reviennent souvent dans les spams mais peuvent aussi apparaitre dans un courrier légitime. Par exemple, les mots « Augmentez »,
« Gains », « Maigrir », « Viagra » « Performance », « Opportunité », « Cash », « Exceptionnel »… ou des groupes de mots comme « Vente privée »
sont parmi les plus fréquents dans un spam, et plus rares dans un courriel légitime. À l’inverse, le nom de vos amis apparaissent fréquemment
dans un courriel légitime et rarement dans un spam.
Le filtre ne connaît pas à l’avance les probabilités de trouver ces mots ou groupes de mots dans un spam ou bien dans un courriel légitime,
et d’ailleurs, ces probabilités dépendent de chaque utilisateur. Il va donc falloir au filtre un temps d’apprentissage pour les évaluer.
Cet apprentissage va être réalisé manuellement par l’utilisateur du logiciel, qui doit indiquer au cas par cas si un message est un spam ou non.
L’ensemble des messages servant à l’apprentissage doit être suffisamment grand et divers, et comporter environ la moitié de spams et la moitié
de courriels légitimes.
4 / 45
Pendant la phase d’apprentissage, pour chaque mot de chaque message rencontré, le filtre ajuste les probabilités de rencontrer ce mot dans un
spam ou un courrier légitime et les stocke dans sa base de données. L’évolution de ces probabilités pourra même se poursuivre tout au long de
l’utilisation du logiciel (même après la phase d’apprentissage).
Après l’apprentissage, lorsqu’un nouveau message arrive dans la boite de réception, les probabilités des mots qui le composent sont utilisées
pour calculer la probabilité que ce message soit un spam.
En pratique, tous les mots appris ne servent pas forcément au calcul de cette probabilité. Un sous-ensemble de mots présents dans le courriel,
donnant les meilleures chances de détecter un spam ou un courriel légitime, et étant les plus fréquents, peuvent être utilisés (une quinzaine
selon Paul Graham).
Un des principaux avantages du filtre bayésien est qu’il s’adapte à son utilisateur, qui peut avoir des centres d’intérêt personnels ou
professionnels sur internet bien différents d’un autre utilisateur.
5 / 45
Partie II - Spamicité
A- Spamicité d’un mot
Mon ordinateur personnel m’indique que j’ai reçu un courriel.
Soit \(S\) l’évènement : « le courriel est un spam » et \(M\) : « le courriel contient le mot
Machin ».
\(P_S (M)\) désigne la probabilité que le mot
Machin figure dans le courriel sachant que c’est un spam. Elle est évaluée par la fréquence des
messages contenant
Machin parmi les messages identifiés comme du spam pendant la phase d’apprentissage.
De même, \(P_\bar{S} (M)\) est évaluée par la fréquence des messages contenant
Machin parmi les messages identifiés comme légitime durant la phase
d’apprentissage.
\(P_M (S)\) désigne la probabilité que le message soit du spam sachant que le mot
Machin y figure.
Cette quantité est appelée spamicité du mot
Machin, et c’est elle que nous allons calculer.
6 / 45
2. Quelle est la bonne réponse ?
8 / 45
3. Quelle est la bonne réponse ?
9 / 45
Puisque \(P_M(S)=\frac{P_S(M)\times P(S)}{P(M)}\) et \(P(M)=P_S(M)\times P(S)+P_\bar{S}(M)\times P(\bar{S})\)
On obtient,
$$P_M(S)=\frac{P_S(M)\times P(S)}{P_S(M)\times P(S)+P_\bar{S}(M)\times P(\bar{S})}$$
C'est ça,
la formule de Bayes !
10 / 45
La plupart des logiciels bayésiens de détection du spam considèrent qu’il n’y a pas de raison a priori qu’un message reçu soit un spam
plutôt qu’un message légitime, et considèrent les deux cas comme ayant des probabilités identiques : \(P(S) = P(\bar{S}) = 0,5\).
Les filtres qui
font cette hypothèse sont dits « non biaisés », ce qui signifie qu’ils n’ont pas de préjugés sur le courrier reçu.
Nous avions \(P_M(S)=\frac{P_S(M)\times P(S)}{P_S(M)\times P(S)+P_\bar{S}(M)\times P(\bar{S})}\)
On obtient :
11 / 45
$$P_M(S)=\frac{P_S(M)}{P_S(M)+P_\bar{S}(M)}$$
Application numérique avec \(P_S (M)=0,05\) et \(P_\bar{S}(M)=0,01\) :
12 / 45
Remarque :
| On rappelle que | $$P_M(S)=\frac{P_S(M)}{P_S(M)+P_\bar{S}(M)}$$ |
Si le mot
Machin n’a jamais été rencontré durant la phase d’apprentissage, le numérateur et le dénominateur sont tous les deux nuls.
Une solution proposée par Paul Graham est de prendre dans ce cas \(P_M(S) = 0,4\).
Comme suggéré dans l’introduction, on peut travailler en pratique avec la dizaine ou quinzaine de mots ayant la spamicité la plus éloignée
de 0,5 (et à égalité de spamicité, avec les mots les plus fréquents).
Ce sont eux les plus intéressants pour déterminer si un courriel est un spam ou non.
13 / 45
Fin de la partie I.
14 / 45
B- Combiner les probabilités individuelles
Nous avons vu comment calculer la spamicité de chaque mot intéressant. Mais comment prendre en compte la spamicité de chaque mot afin de déterminer la spamicité conjointe
de tous les mots, c’est-à-dire la probabilité d’être un spam sachant que tous ces mots apparaissent dans le message ?
Eh bien, cela peut paraitre compliqué, mais en faisant une hypothèse abusive, on va voir que l’on peut obtenir une jolie formule. Le filtrage bayésien
naïf du spam fait l’hypothèse que les présences de chaque mot intéressant dans le message sont des évènements indépendants. Cela est faux dans les langages naturels comme
le français, où la probabilité de trouver un adjectif, par exemple, est influencée par la probabilité d’avoir un nom. Voilà l’origine du mot naïf employé.
15 / 45
Quoi qu'il en soit, avec cette hypothèse naïve, on va déduire une autre formule de celle de Bayes qui s’avère être en pratique très efficace…
Prenons deux mots
intéressants.
Soit \(p_1 = P_{M_1}(S)\) la spamicité du mot 1 et \(p_2 = P_{M_2} (S)\) la spamicité du mot 2.
Notons \(p = P_{M_1\cap M_2} (S)\) la spamicité conjointe des mots 1 et 2.
Voyons voir comment peut-on aboutir à une formule donnant \(p\) en fonction de \(p_1\) et \(p_2\).
On rappelle l’hypothèse \(P(S) = P(\bar{S}) = 0,5\) et \(M_1, M_2\) indépendants.
On s’accroche car cela va être un peu ardu…
16 / 45
Compléter les champs suivants par la lettre qui correspond à la réponse :
17 / 45
Or pour tout mot \(M\) :
18 / 45
On obtient donc :
\(P_{M_1\cap M_2} (S) = \frac{P_S(M_1\cap M_2)}{P_S (M_1\cap M_2) + P_\bar{S}(M_1\cap M_2)} = \frac{P_S (M_1)P_S (M_2)}{P_S (M_1)P_S (M_2) + P_\bar{S}(M_1)P_\bar{S}(M_2)} \)
\( = \frac{2\times P_{M_1} (S)\times P(M_1)\times 2\times P_{M_2} (S)\times P(M_2)}{2\times P_{M_1} (S)\times P(M_1)\times 2\times P_{M_2} (S)\times P(M_2)+2\times (1- P_{M_1} (S))\times P(M_1)\times 2\times (1- P_{M_2} (S))\times P(M_2)} \)
\( =\frac{P_{M_1}(S)\times P_{M_2}(S)}{P_{M_1}(S)\times P_{M_2}(S)+(1- P_{M_1}(S))\times (1- P_{M_2}(S))} \) (en divisant numérateur et dénominateur par \(4P(M_1)P(M_2)\))
\(P_{M_1\cap M_2}(S) =\frac{p_1 \times p_2}{p_1 \times p_2 + (1- p_1)\times (1- p_2)}\).
19 / 45
En généralisant à un ensemble de \(N\) mots utilisés, on obtient exactement de la même manière la jolie formule suivante :
$$p = P_{M_1\cap M_2\cap …\cap M_N}(S)= \frac{p_1 \times p_2 \times …\times p_N}{p_1 \times p_2 \times …\times p_N + (1- p_1)\times (1- p_2)\times …\times (1- p_N)} $$
Application numérique : calcul de la spamicité conjointe de 3 mots : \(p_1 = 0,7\) ; \(p_2 = 0,2\) ; \(p_3 = 0,9\)
20 / 45
$$p = \frac{p_1 \times p_2 \times …\times p_N}{p_1 \times p_2 \times …\times p_N + (1- p_1)\times (1- p_2)\times …\times (1- p_N)} $$
Dans la
partie III, on va transformer cette formule en une autre qui est plus facile à utiliser avec une machine et qui ne produit pas en principe de dépassement
de capacité comme cela peut être le cas avec la multiplication d’un grand nombre de valeurs « petites ».
En pratique, on compare la valeur de \(p\) à un seuil donné pour décider si l’on classe ou non le message comme spam. Cependant, un certain nombre de messages peuvent
se retrouver ainsi mal classés : ce sont les faux positifs et les faux négatifs (voir
Partie IV- Faux positifs, faux négatifs - Seuil).
21 / 45
Partie III – Changement de formule
Dans la
partie II, on a vu que la probabilité pour un message d’être un spam sachant qu’il contient \(N\) mots donnés est fournie par la formule :
$$p = P_{M_1\cap M_2\cap …\cap M_N}(S)= \frac{p_1 \times p_2 \times …\times p_N}{p_1 \times p_2 \times …\times p_N + (1- p_1)\times (1- p_2)\times …\times (1- p_N)}$$
Cette formule permettant de déterminer \(p\) en fonction des \(p_i\) possède un inconvénient lorsqu’on la calcule informatiquement, avec un « grand »
nombre de probabilités à combiner.
En effet, le produit d’un grand nombre de valeurs au voisinage de zéro peut donner un nombre trop petit pour pouvoir être stocké. C’est ce qu’on appelle un dépassement de capacité par valeurs inférieures (appelée parfois soupassement arithmétique).
Un remède est de ramener le calcul d’un produit à un calcul de somme et faire émerger une autre formule permettant de calculer \(p\) en fonction des \(p_i\).
On va donc utiliser la fonction logarithme…
Veuillez noter cette formule pour la suite.
23 / 45
En posant
$$a_N=\sum_{i=0}^N \left(\ln(1-p_i)-\ln(p_i)\right)$$
on en déduit :
26 / 45
Un autre avantage de cette formule est qu’elle permet une programmation facile :
Compléter l’algorithme suivant :
| Rappel : | $$a_N=\sum_{i=0}^N \left(\ln(1-p_i)-\ln(p_i)\right)$$ | et | $$p=\frac{1}{1+e^{a_N}}$$ |
\(L = [p_1\) \(p_2\) \( … \) \(p_N]\)
// \(L\) liste contenant les \(N\) probabilités \(p_k\).
// \(L[i]\) est le \((i + 1)^e\) terme de la liste. Par exemple \(L[0]\) est \(p_1\).
Début Algorithme
\(a\) prend la valeur 0
27 / 45
Partie IV- Faux positifs, faux négatifs - Seuil
Dans la
partie II, on a vu que la probabilité pour un message d’être un spam sachant qu’il contient \(N\) mots donnés est fournie par la formule
\(p = P_{M_1\cap M_2\cap …\cap M_N}(S)= \frac{p_1 \times p_2 \times …\times p_N}{p_1 \times p_2 \times …\times p_N + (1- p_1)\times (1- p_2)\times …\times (1- p_N)}\).
Grâce au résultat trouvé, le logiciel bayésien va décider si le message en question est un spam ou non et ceci en comparant \(p\) à un seuil \(s\) :
Si \(p>s\) alors on classe le message comme étant un spam et sinon on le classe comme légitime.
Cependant le filtre peut se tromper, en décidant par exemple que le message est un spam alors qu’il ne l’est pas, ou bien en décidant que c’est un message légitime
alors que c’est un spam.
Un « faux positif » est un message légitime classé par erreur comme spam, et un « faux négatif » est un spam classé par erreur comme message légitime (à rapprocher
d’un test diagnostic en médecine).
28 / 45
On pourrait être tenté de prendre \(s = 0,5\), c’est-à-dire que si on a plus d’une chance sur deux que le message soit un spam, on le classe comme tel. Dans ce cas,
on imagine bien que « beaucoup » de messages vont être déclarés spam, donc un maximum de vrais spams mais aussi un certains nombres de messages légitimes.
Faire cela minimise donc les faux négatifs mais peut rendre fréquents les faux positifs.
Inversement, on pourrait être tenté de prendre \(s\) « grand », par exemple \(s = 0,99\). Dans ce cas, le seuil pour être déclaré spam est bien plus sévère, donc on aura
beaucoup moins de faux positifs, mais plus de faux négatifs.
29 / 45
Ceci dit, il est bien plus dommageable dans la plupart des cas d’avoir des faux positifs que des faux négatifs.
En effet, plus le filtre anti spam sera efficace pour bloquer les spams, moins l’utilisateur va vérifier son répertoire de spams car sa confiance dans le logiciel
sera accrue. Les fois où il va vérifier ce dernier, ses courriers légitimes vont être noyés dans la masse de spams détectés.
Il est acceptable d’autoriser quelques faux négatifs à supprimer à la main ; ça l’est beaucoup moins d’avoir des faux positifs importants non lus ou tout bonnement
supprimés.
Si on essaie de quantifier cette différence, en considérant par exemple que l’existence de faux positifs est \(\lambda\) fois plus « coûteux » que celle de faux négatifs, on
classifie alors un message comme étant un spam si \(\frac{p}{q}>\lambda\) ; avec \(p = P_{M_1\cap M_2\cap …\cap M_N}(S)\) et \(q = P_{M_1\cap M_2\cap …\cap M_N} (\bar{S}) = 1-p\).
Cela signifie que bloquer un courriel légitime est comparable à laisser passer \(\lambda\) spams à travers le filtre.
30 / 45
On souhaite choisir \(\lambda\) tel que \(\frac{p}{q}>\lambda\) avec \(q = 1-p\).
Cela signifie que :
31 / 45
Le seuil \(s\) en fonction de \(\lambda\) est donc \(s = \frac{\lambda}{1 + \lambda }\)
32 / 45
Le choix du seuil est laissé à l’utilisateur qui doit l’ajuster à vue de nez selon ses exigences. On choisit un seuil assez important surtout dans les
cas où l’on supprime tout de suite un courriel considéré comme étant un spam; dans ce cas, classifier un courrier légitime comme étant un spam signifierait
perdre ce courriel.
Cependant, aujourd’hui on utilise souvent des valeurs de \(\lambda\) moins importantes et on ne supprime pas tout de suite le spam. Le spam est souvent mis dans un
répertoire pour une durée déterminée avant sa suppression définitive.
33 / 45
On a vu que le choix d’un seuil laissait de toute manière passer plus ou moins de faux positifs et de faux négatifs à travers le filtre.
Voici par exemple les résultats de classement de 1 000 messages légitimes et de 5 000 spams par un logiciel anti-spam.
| Message légitime | Spam |
|---|
| Classement « message légitime » | 982 (VN) | 487 (FN) |
|---|
| Classement « spam » | 11 (FP) | 4 875 (VP) |
|---|
VN nombre de vrais négatifs ; FN nombre de faux négatifs ;
VP nombre de vrais positifs ; FP nombre de faux positifs.
34 / 45
Voici des indicateurs que l’on peut déduire du tableau précédent et que l’on peut trouver dans une évaluation d’un filtre anti-spam :
- Le taux d’erreur par classe (faux positifs et faux négatifs)
Il s’agit du quotient du nombre de messages d’une catégorie classés par erreur dans l’autre classe :
\(FPR = \frac{FP}{VN+FP} \) (false positive rate) \(FNR = \frac{FN}{VN+FN} \) (false negative rate)
Ces taux ont l’avantage de ne pas dépendre de la répartition message légitimes/spam.
- Le taux de bon classement :
\(TNR = \frac{VN}{VN+FP}=1-FPR \) (true negative rate ou spécificité)
\(TPR = \frac{VP}{VP+FN}=1-FNR \) (true positive rate ou sensibilité)
Pour l’exemple donné :
35 / 45
Fin de la partie IV.
36 / 45
Partie V - Un mot sur SpamAssassin
Pour étudier le corps d’un message, certains filtres anti-spam utilisent, en plus d’un filtre bayésien, d’autres tests, non probabilistes, mais basés sur la
recherche d’expressions type utilisées dans les spams. Ces logiciels utilisent ce qu’on appelle des expressions rationnelles (voir ailleurs pour plus de détails)
pour vérifier si oui ou non une phrase qui est multiforme apparait dans les messages. Une phrase multiforme est une phrase qui s’écrit avec les mêmes mots (ou synonyme),
accent ou non, mais qui n’a pas la même syntaxe.
En plus d’un test bayésien, existent donc un certains nombres de règles prédéfinies, dans divers catégories (lois, santé, marketing...) qui sont dotés comme le test de
Bayes d’un score qui s’ajoutent à celui-ci si elles sont vérifiées.
C’est par exemple le cas pour le logiciel anti-spam (gratuit) SpamAssassin.
37 / 45
Exemples de règles pour la France crées pour SpamAssassin par John Gallet, fondateur de la société Saphir Tech (nous avons choisi les scores) :
| # Spam is legal in France ! | |
| body FR_SPAMISLEGAL | /\b(Conform.+ment|Envertu).{0,5}(article.{0,4}34.{0,4})?la loi\b/i |
| describe FR_SPAMISLEGAL | French: pretends spam is (l)awful. |
| langfrdescribe FR_SPAMISLEGAL | Invoque la loi informatique et libertes. |
| score FR_SPAMISLEGAL | 1 |
| |
| |
| body FR_SPAMISLEGAL_2 | /\bdroit d.acc.+s.{1,3}(de modification)?.{0,5}de rectification\b/i |
| describe FR_SPAMISLEGAL_2 | French: pretends spam is (l)awful. |
| langfrdescribe FR_SPAMISLEGAL_2 Invoque le droit de rectification cnil. |
| score FR_SPAMISLEGAL_2 | 1 |
| |
| |
| # How to unsubscribe | |
| |
| |
| body FR_HOWTOUNSUBSCRIBE | /\b(souhaitez|d.+sirez|pour).{1,10}(plus.{1,}recevoir|d.+sincrire|d.+sinscription|d.+sabonner).{0,10} |
| (information|email|mail|mailing|newsletter|lettre|liste|message|offre|promotion|programme)(s)?\b/i |
| describe FR_HOWTOUNSUBSCRIBE | French: how to unsubscribe |
| langfrdescribe FR_HOWTOUNSUBSCRIBE | Indique comment se desabonner. |
| score FR_HOWTOUNSUBSCRIBE | 2.0 |
38 / 45
Exemple d’entête ajoutée à un message filtré par le logiciel SpamAssassin :
X-Spam-Level: *********
X-Spam-Status: Yes, score=9.0 required=5.0 tests=BAYES_99,FROM_EXCESS_BASE64,
FR_HOWTOUNSUBSCRIBE,FR_SPAMISLEGAL,FR_SPAMISLEGAL_2,HK_RANDOM_ENVFROM,
HTML_IMAGE_RATIO_04,HTML_MESSAGE,UNPARSEABLE_RELAY autolearn=no version=3.3.1
X-Spam-Report:
* 3.5 BAYES_99 BODY: Bayes spam probability is 99 to 100%
* [score: 1.0000]
* 0.0 HK_RANDOM_ENVFROM Envelope sender username looks random
* 1.0 FR_SPAMISLEGAL_2 BODY: French: droit d acces de modification de
* rectification
* 2.0 FR_HOWTOUNSUBSCRIBE BODY: French: how to unsubscribe
* 1.0 FR_SPAMISLEGAL BODY: French: Conformement ou En vertu....la loi
* 0.6 HTML_IMAGE_RATIO_04 BODY: HTML has a low ratio of text to image area
* 0.0 HTML_MESSAGE BODY: HTML included in message
* 1.0 FROM_EXCESS_BASE64 From: base64 encoded unnecessarily
* 0.0 UNPARSEABLE_RELAY Informational: message has unparseable relay lines
Le score de ce message est 9.
39 / 45
Il faut dépasser un score de 5 pour que SpamAssassin déclare le message comme spam. Le filtre bayésien apporte le score maximal de 3,5 (voir après) ; à lui
seul il ne suffit donc pas ; il faut donc qu’au moins une autre règle (prédéfinie) soit vérifiée pour être déclaré spam. Si le score final est entre 5 et 15,
le message ira dans un répertoire spécifique dont il faudra extraire à la main les faux positifs. Si le score dépasse 15, le message ira directement à la poubelle.
Avant d’appliquer un filtre bayésien et des règles supplémentaires prédéfinies sur le corps du message, existent d’autres filtres, comme le filtrage d’enveloppe du
message, c’est-à-dire l’analyse de l’en-tête du courriel, qui contient un certains nombres d’informations de base : expéditeur, destinataire, copie conforme, copie
conforme invisible, date d’envoi, serveur source, sujet... L’existence d’une liste blanche (expéditeurs reconnus comme légitimes) et/ou d’une liste noire (expéditeurs
reconnus de spams) peut alors s’avérer très efficace. SpamAssassin attribue par exemple respectivement un score de 100 ou -100 à ces deux listes.
40 / 45
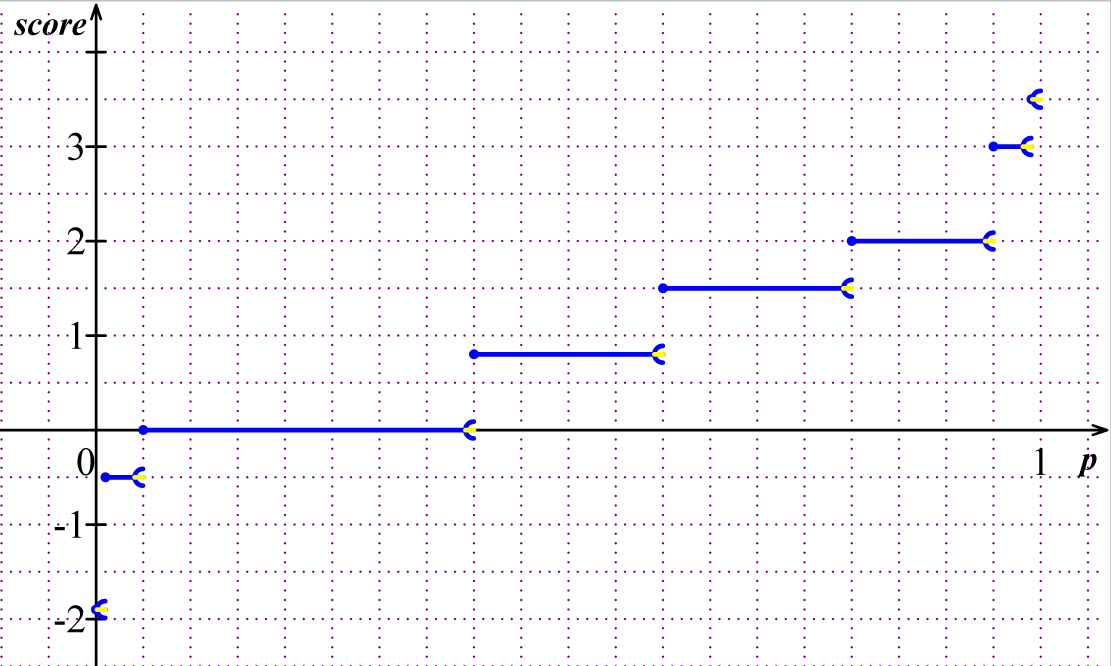
Attribution d’un score à la probabilité issue du test de Bayes, par SpamAssassin :
| BAYES_00 | \(p \in [0 ; 0,01[\) | score -1,9 |
| BAYES_05 | \(p \in [0,01 ; 0,05[\) | score -0,5 |
| BAYES_20 | \(p \in [0,05 ; 0,20[\) | score -0,001 |
| BAYES_40 | \(p \in [0,20 ; 0,40[\) | score -0,001 |
| BAYES_50 | \(p \in [0,40 ; 0,60[\) | score 0,8 |
| BAYES_60 | \(p \in [0,60 ; 0,80[\) | score 1,5 |
| BAYES_80 | \(p \in [0,80 ; 0,95[\) | score 2,0 |
| BAYES_95 | \(p \in [0,95 ; 0,99[\) | score 3,0 |
| BAYES_99 | \(p \in [0,99 ; 1]\) | score 3,5 |
41 / 45
Compléter l’algorithme suivant :
\(P = [0\) \( 0,01\) \( 0,05\) \( 0,2\) \( 0,4\) \( 0,6\) \( 0,8\) \( 0,95\) \( 0,99] \)
// \(P\) liste des seuils de changement de score
\(S = [-1,9\) \( -0,5\) \( -0,001\) \( -0,001\) \( 0,8\) \( 1,5\) \( 2\) \( 3\) \( 3,5] \)
// \(S\) liste contenant les scores.
// Rappel : \(S[i]\) est le \((i + 1)^e\) terme de la liste. Par exemple \(S[0]\) est -1,9.
Début Algorithme
Saisir \(p\).
42 / 45
La fonction score issue du test bayésien de SpamAssassin est un exemple de fonction non continue.
43 / 45
Remerciements
Merci à John Gallet, de la société Saphir Tech, pour ses explications précises sur le logiciel SpamAssassin, et la mise en ligne de règles complémentaires
pour la France.
Merci à Abdellatif KBIDA pour ses explications supplémentaires à propos du document d’accompagnement d’ISN « Le filtrage du spam », qu’il a réalisé avec l’aide
de Yannick PARMENTIER, maître de conférence de l’université d’Orléans, laboratoire d’informatique fondamentale et de Valéry FEBVRE, chef de projet, société Easter-eggs.
45 / 45