Le classement Elo
 Niveau
Niveau : terminale générale, Maths complémentaires, mais avec des éléments dans seulement l'un des deux programmes, ou hors des deux programmes.
Lien avec le programme : suites, probabilités, densités de probabilités, modèle logistique, algorithmique.
Lien avec Les maths au quotidien : Sport, Loisirs.
1 / 33
Tout le monde connait, au moins de nom, le classement ATP au tennis, ou bien le classement FIFA pour le football.
Dans la plupart des sports, ainsi que dans des disciplines compétitives comme les Échecs, il existe différents systèmes de classements,
qui permettent de hiérarchiser les joueurs ou les équipes suivant leur « force ».
Lors d’un match entre deux joueurs ou équipes, il y a souvent un favori et un outsider, et nous avons une idée « intuitive » des chances de
victoire de tel joueur face à l’autre.
Quelques citations, entendu ici ou là, pour étayer mon propos :
« Tu vas voir, il va lui mettre une sacrée tannée »
« La vie de ma reum qu’y a match nul ».
2 / 33
Dans les années 1960, le physicien américain Arpad Elo, également joueur d’échecs de niveau international, a mis au point un système de
classement qui porte son nom :
le classement Elo.
Ce système est, comme on va le voir, une méthode de calcul de la force relative de deux joueurs et est utilisé actuellement dans de nombreux
jeux et sports, tels le jeu d’échecs, le jeu de Go, le baseball, le football américain universitaire, le football féminin mondial, ainsi que
dans de nombreux jeux en ligne sur Internet.
3 / 33
Dans les grandes lignes, Elo proposa de donner à tout joueur un classement, un nombre généralement compris entre 1 000 pour les débutants et
2 800 pour les meilleurs joueurs du monde, et de réajuster ce classement à la hausse ou à la baisse à l’issue de chaque partie, en fonction
du résultat du joueur.
Mais la force d’un joueur ne se résume pas tout-à-fait à son classement. On sait bien qu’un joueur peut être dans un mauvais ou un bon jour,
selon son état physique et/ou psychologique et il peut jouer certaines parties tantôt au-dessus, tantôt en dessous de son niveau.
Ainsi Elo jugea que le niveau d’un joueur pouvait être modélisé par une variable aléatoire normale, centrée sur son classement, et d’écart-type
200 pour tous les joueurs. Ainsi par exemple, selon une propriété bien connue de la loi normale, un joueur possédant un classement de 1 500
jouera environ 68 % de ses parties à un niveau compris entre 1 300 et 1 700.
On va voir que ce système permet d’associer la probabilité de victoire d’un joueur avec la différence de points au classement avec son
adversaire.
4 / 33
Voyons ce système de manière plus détaillée :
Dans ce système, lorsqu’un joueur bat un autre joueur, son classement est, de manière naturelle, vu à la hausse de façon proportionnelle
à la différence des classements (très peu d’augmentation si le joueur était très favori, une grande augmentation s’il était grand outsider),
et de même, le classement de son adversaire est revu à la baisse du même nombre de points.
5 / 33
Dans un premier temps, nous allons supposer que nous avons deux joueurs qui jouent toujours ensemble : Garry et Anatoly.
Arpad Elo propose le procédé suivant pour donner un classement à chaque joueur :
Soit \(r_1\) le classement initial de Garry (on verra plus loin comment il est donné) et \(r_n\) son classement avant la \(n\)-ième partie.
Alors \(r_{n + 1} = r_n + G_n\), où \(G_n\) est le nombre de points Elo obtenus par Garry lors de la \(n\)-ième partie.
\(G_n\) peut être négatif et si Garry obtient \(G_n\) points, Anatoly en obtient \(-G_n\).
6 / 33
Plaçons-nous à une partie donnée. On renote \(r’ = r + G\) où \(r\) est le classement de Garry avant la partie, \(r’\) son classement après la partie
et donc \(G\) le nombre de points qu’il va obtenir pendant cette partie.
On va noter \(s\) le score de Garry lors de cette partie : 1 si Garry gagne, 0 s’il pert et 0,5 s’il y a match nul.
Le score d’Anatoly est donc \(1 - s\).
7 / 33
Arpad Elo introduit alors la notion de « score espéré », ou « probabilité de gain » de Garry lors de la partie, qui ne dépend que de la
différence de classement \(D\) entre Garry et Anatoly juste avant cette partie.
On va noter \(p(D)\) cette probabilité de gain (ce score espéré) en fonction de la différence de classement.
Plus la différence de classement \(D\) est grande et plus la probabilité de gain de Garry est grande et s’approche de 1, mais aussi, elle
s’approche de 0 si cette différence est de plus en plus grande en valeur absolue mais en étant négative.
En considérant que la différence de niveau de deux joueurs quelconques est une variable continue, quelle loi de probabilité choisir ? Il existe en effet une infinité
de lois continues et même une infinité de fonctions densités de probabilité.
8 / 33
Déjà, essayons de choisir une densité de probabilité.
Arpad Elo propose que le gain \(G\) soit proportionnel à l’écart entre le score obtenu et le score espéré. C’est raisonnable car un écart
important signifie que les joueurs ont un niveau très différent, et il faut de manière conséquente payer la victoire du plus faible et
sanctionner la défaite du plus fort ; alors que deux joueurs de niveaux proches ne doivent pas voir leurs classements beaucoup évoluer…
9 / 30
On a ainsi le calcul du gain algébrique du classement de Garry :
\(G = K(s - p(D))\) où \(K\) est un coefficient fixé à l’avance, et dont on parlera plus loin.
Celui d’Anatoly est donc : \(-G = K(1 - s - p(-D))\)
En effet si Garry obtient \(G\) points, Anatoly en obtient \(-G\), si le score de Garry est \(s\), celui d’Anatoly est \(1 - s\) et si la différence
de classement entre Garry et Anatoly est \(D\), celle entre Anatoly et Garry est \(-D\).
On obtient alors \(K(s - p(D)) = -K(1 - s - p(-D))\), soit \(p(-D) = 1 - p(D)\).
On a donc \(p(-x) = 1 - p(x)\) pour tout \(x\) réel.
10 / 33
Cela implique que la densité de probabilité cherchée est symétrique par rapport à l’axe des ordonnées…
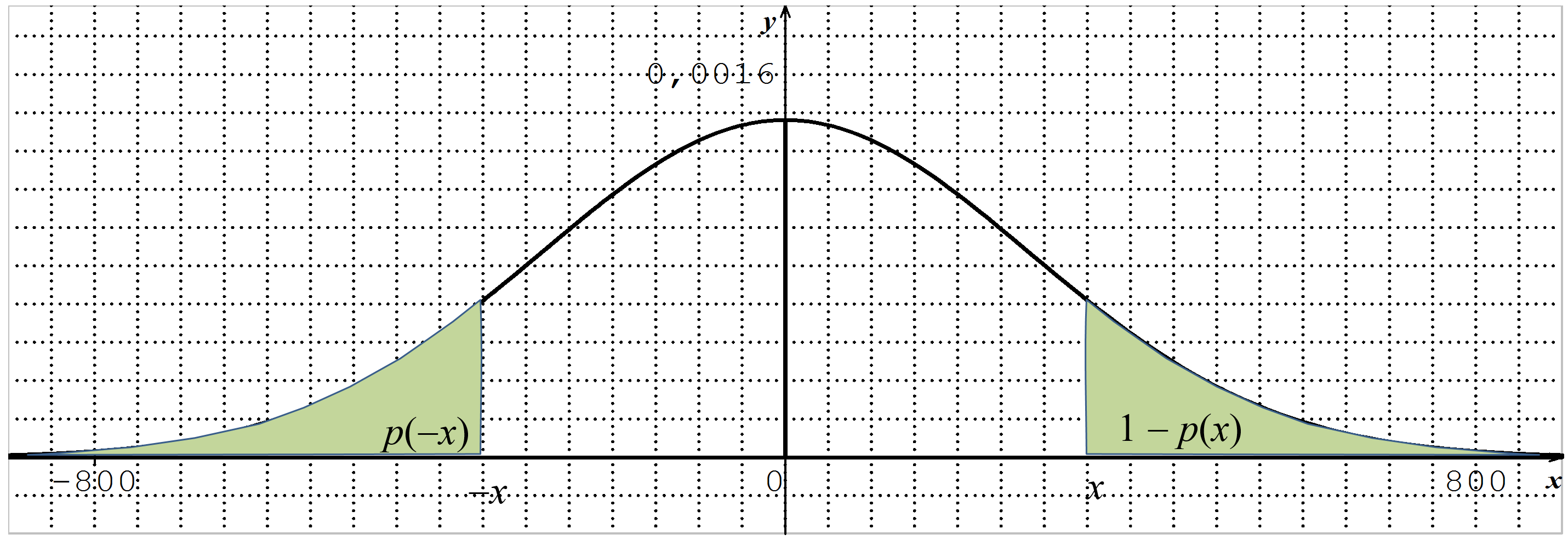
11 / 33
Historiquement, Arpad Elo a choisi une loi normale \(N(0 \,; (200\sqrt{2} )^2)\) pour modéliser son score espéré.
Il a choisi \(200\sqrt{2}\), de sorte qu’une différence de 200 points sur le classement amène une probabilité de victoire d’environ 75 %
(en fait cela vient du fait que le niveau d’un joueur est pour Elo une variable aléatoire normale, centrée en son classement, et
d’écart-type 200, voir l’aparte ci-dessous).
Voyons voir maintenant si cette loi normale est vraiment bien adaptée…
Plaçons-nous toujours à une partie donnée de la compétition.
Aparte : soit \(S\) une variable aléatoire de loi normale \(N(0 \,; (200\sqrt{2})^2)\). Déjà on peut vérifier que \(P(S \le 200) \approx 0,76 \approx 75\ \%\).
Ensuite, pour deux joueurs avant une rencontre, soient \(N_1\) le niveau du joueur 1 et \(N_2\) le niveau du joueur 2, et \(N\) la variable aléatoire différence de niveau : \(N = N_2 - N_1\).
Comme \(N_1\) et \(N_2\) sont pour Elo des variables aléatoires normales d'écart-type 200, que l'on peut clairement considérer indépendantes, alors \(N\) suit une loi normale d’écart-type \(\sqrt{200^2 + 200^2} = 200\sqrt{2}\).
12 / 33
Supposons que l’on ait désormais trois joueurs qui s’affrontent : Garry, Anatoly et Bobby.
Une question naturelle est la suivante : connaissant la probabilité de gain de Garry contre Anatoly, ainsi que celle d’Anatoly contre Bobby,
quelle est la probabilité de gain de Garry contre Bobby ?
Si deux joueurs ont disputé entre eux un nombre significatif de parties, on peut facilement définir la notion de force relative entre ces
deux joueurs.
Introduisons la notion de force relative de Garry contre Anatoly.
13 / 33
Supposons que Garry joue un nombre N très grand de parties contre Anatoly. On rappelle qu’une victoire rapporte 1 point, un match nul
0,5 point et une défaite 0 point.
On note \(N_G\) le nombre de points gagnés par Garry (la somme de ses scores sur les \(N\) parties) et \(N_A\) le nombre de points gagnés par Anatoly.
On a alors \(N_G + N_A = N\).
La probabilité de gain de Garry contre Anatoly est : $$p = \frac{N_G}{N} $$
14 / 33
On appelle
force relative de Garry contre Anatoly la quantité \(\frac{N_G}{N_A}\), soit tout calcul fait \(\large \frac{p}{1-p}\).
On la note \(f(p)\).
De la même manière, on note \(q\) et \(f(q)\) respectivement la probabilité de gain et la force relative d’Anatoly contre Bobby et
\(r\), \(f(r)\) respectivement la probabilité de gain et la force relative de Garry contre Bobby.
On a : $$f(q) = \frac{q}{1-q}$$ et $$f(r) = \frac{r}{1-r}$$
15 / 33
Maintenant, raisonnons en termes de forces : si Garry est deux fois plus fort qu’Anatoly et si Anatoly est trois fois plus fort
que Bobby alors il est naturel de dire que Garry est six fois plus fort que Bobby.
La force est multiplicative : la force de Garry contre Bobby est égale au produit des forces intermédiaires, celle de Garry contre
Anatoly par celle d’Anatoly contre Bobby : \(f (r) = f (p) \times f (q)\), c’est-à-dire :
$$ \frac{r}{1-r}= \frac{p}{1-p} \times \frac{q}{1-q} $$
16 / 33
Or, le classement que nous construisons est un classement additif, pour lequel l'écart entre Garry et Bobby doit être égal à la somme
des écarts entre Garry et Anatoly d'une part et Anatoly et Bobby d'autre part, ce qui n'est pas le cas avec le produit des forces.
En notant \(D(p)\), \(D(q)\), \(D(r)\) les différences de classement respectivement entre Garry et Anatoly, Anatoly et Bobby, Garry et Bobby,
on cherche donc une fonction \(h\) telle que :
\(D(p) = h(f (p))\), \(D(q) = h(f (q))\) et \(D(r) = h(f (r))\) et telle que \(D(r) = D(p) + D(q)\).
Cela signifie que \(h(f (r)) = h(f (p)) + h(f (q))\).
Comme \(f (r) = f (p) × f (q)\), on obtient \(h(f (p) × f (q)) = h(f (p)) + h(f (q))\).
17 / 33
Cette transformation par \(h\) d’un produit en somme caractérise les fonctions logarithmes.
Choisissons par exemple la fonction logarithme décimale pour \(h\).
On obtient :
$$D(p) = \log(f (p)) = \log \left(\frac{p}{1-p}\right)$$
Afin de se rapprocher du choix initial d’Arpad Elo qui avait pris une loi normale \(N(0 \, ; (200\sqrt{2})^2)\) pour son score espéré
(qui faisait correspondre \(D(p) = 200\) à \(p \approx 0,76\)), un facteur multiplicatif fixé à 400 est introduit.
On obtient la
formule Elo : \(D = 400 \log\left(\large \frac{p}{1-p}\right)\)
18 / 33
Exemple
Avec \(p = 0,60\) et \(q =\large \frac{2}{3} \), les forces sont \(f (p) = 1,5\) ; \(f (q) = 2\) et \(f (r) = 3\).
$$D(p) = 400 × \log (1,5) \approx 70 \:; D(q) = 400 × \log (2) \approx 120 \: ; D(r) = 400 × \log (3) \approx 191$$
Cette égalité permet d’écrire la probabilité de gain \(p\), renotée \(p(D)\), de Garry contre Anatoly en fonction de la différence de
classement \(D\) :
$$p(D) = \frac{1}{1+10^{-\frac{D}{400}}} $$
C'est cette formule qui est utilisée aux Échecs dans le calcul du classement des joueurs.
19 / 33
Exemple
Si deux joueurs ont une différence de classement \(D\) de 50, alors :
$$p = \frac{1}{1+10^{-\frac{50}{400}}} \approx 0,57 $$ et $$f (p) \approx 1,33$$
Le favori a environ 57 % de chance de gagner la partie et il est environ 1,33 fois plus fort que l’autre.
L’une des particularités très intéressantes de ce système est aussi qu’il permet de donner les probabilités de gains de deux adversaires
qui ne se sont jamais rencontrés.
20 / 33
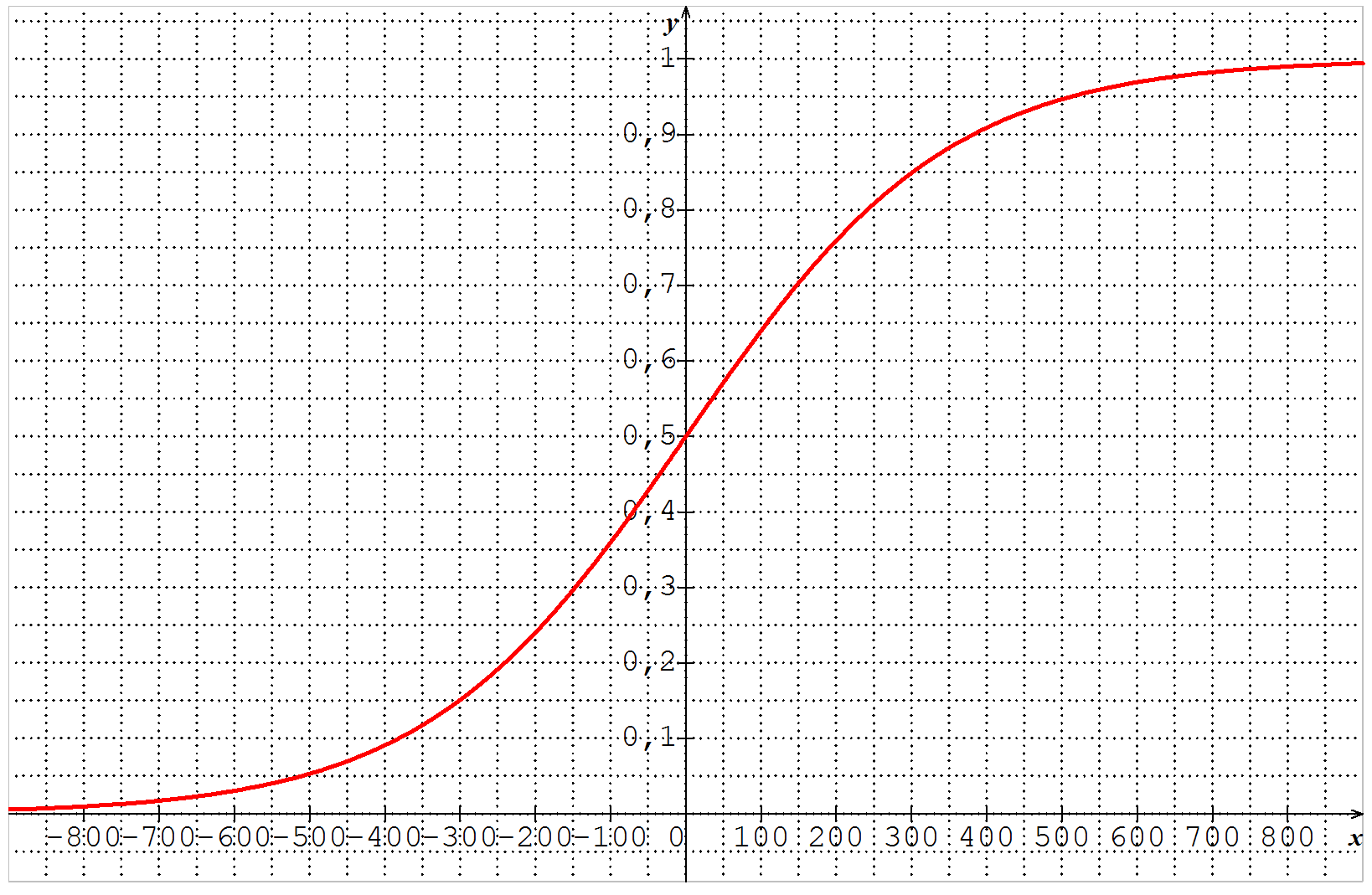
La loi obtenue pour le score espéré n’est donc pas une loi normale mais une autre loi, dite « logistique ».
Remarque : on rencontre ce type de courbes logistiques dans le modèle de Verhulst (dynamique de populations, voir l’ouvrage
«
Les maths au quotidien»).
21 / 33
Regardons rapidement la différence entre les deux densités de probabilités, celle de la loi normale \(N(0 \, ; (200\sqrt{2} )^2)\) et celle de la loi
logistique utilisée ici :
Puisque $$p(D) = 0,5 + \int_0^D g(x)dx$$ où \(g\) est la densité de cette loi logistique, on a :
$$g(D) = p’(D) = \frac{\frac{\ln(10)}{400}10^{-\frac{D}{400}}}{\left(1+10^{-\frac{D}{400}} \right)^2}$$
22 / 33
Voici la différence entre les deux densités (normale en rouge et logistique en bleu) :
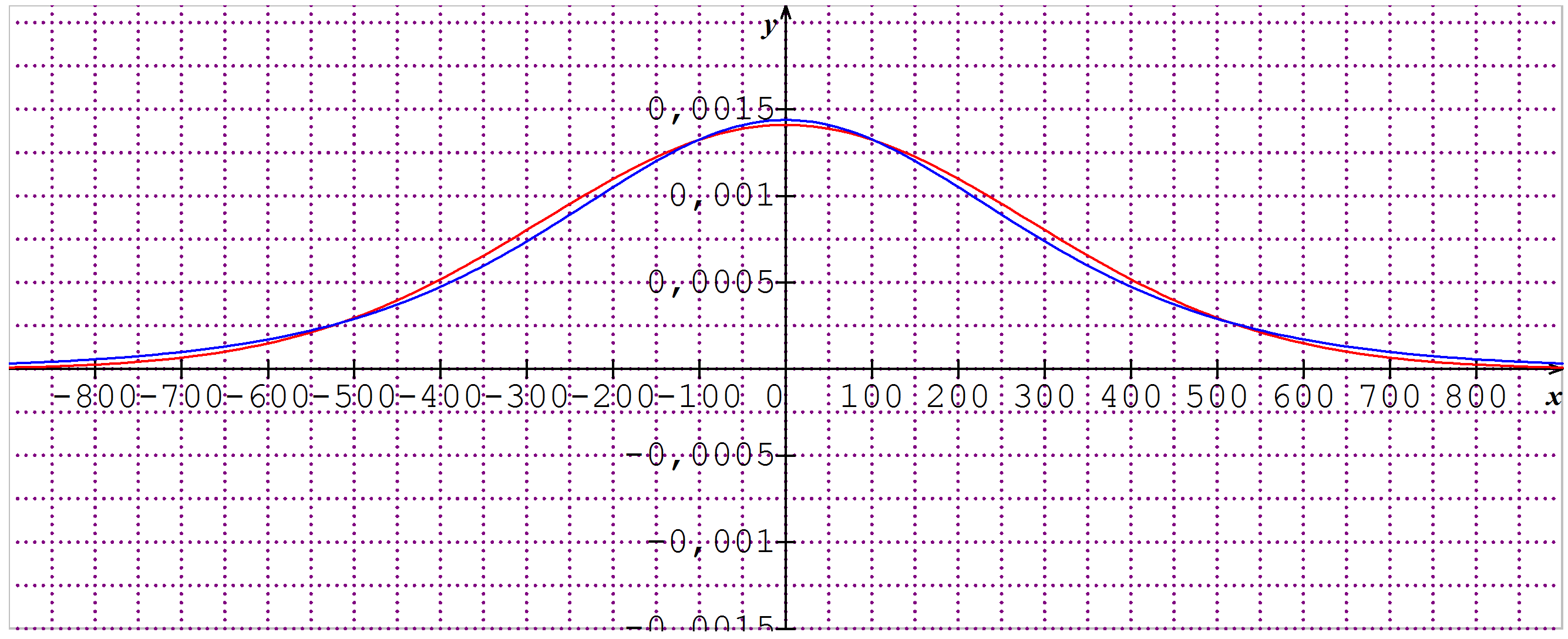
23 / 33
Revenons maintenant à nos moutons initiaux :
Après une partie donnée, le nouveau classement Elo de Garry est \(r’ = r + K (s - p(D))\).
\(r\) est l’ancien classement de Garry, avant la partie, \(s = 1\) si Garry gagne la partie, 0,5 pour un nul et 0 pour une défaite.
$$p(D)=\frac{1}{1+10^{-\frac{D}{400}}}$$
est le score espéré de Garry pour cette partie en fonction de sa différence de classement avec l’autre joueur avant la partie.
\(K\) est un paramètre permettant de « régler » la vitesse d’évolution du classement du joueur. Pour permettre aux nouveaux joueurs
entrants dans le classement de progresser rapidement vers leur niveau réel, K est égal à 30 pour les 30 premières parties. Ensuite \(K\)
est égal à 15 pour les joueurs n’ayant pas atteint 2 400 points. Ensuite \(K = 10\) (même si le joueur redescend en dessous de 2 400).
Le résultat du calcul du nouveau classement est arrondi à l’entier le plus proche.
24 / 33
En pratique la FIDE limite ses calculs en plafonnant \(D\) à 400 points, c’est-à-dire que s’il y a plus de 400 points d’écart, donc plus de 91 %
de probabilité de gain, la différence \(D\) est ramenée à 400 points.
De plus, on ne conserve pas de classement Elo si on descend en dessous de 1 000 points. À ce moment-là, on perd son classement et il faut se
reclasser.
Historiquement à l’initialisation du processus en 1970, il fut décidé que tous les grands maîtres internationaux du monde avaient un classement
de 2 500 points Elo. C’est à partir de cette base initiale de joueurs que le classement s’est progressivement calculé pour tous les autres
joueurs.
25 / 33
Exemple
Un joueur classé 1 500 joue contre un joueur classé 1 755.
$$D = 1\, 500 - 1 755 = -255$$
Le joueur a une probabilité de gain de \(p(D) = 0,18726231836\)
-
En faisant match nul, \(s = 0,5\), avec \(K = 15\), cela lui donne un nouveau classement :
$$r’ = 1\, 500 + 15 (0,5 - 0,18726231836) \approx 1\, 505$$
Le joueur gagne 5 points Elo tandis que son adversaire en perd 5.
-
En gagnant la partie, \(s = 1\), avec \(K= 15\), cela lui donne un nouveau classement :
$$r’ = 1\, 500 + 15 (1 - 0,18726231836) \approx 1\, 512$$
Le joueur gagne 12 points Elo tandis que son adversaire en perd 12.
26 / 33
Détermination du premier classement d’un joueur
Le premier classement d’un joueur est issu d’une procédure un peu complexe que l’on va résumer.
Un joueur va être classé dès qu’il a joué au moins 9 parties contre des joueurs classés, sur un ou plusieurs tournois. Dans chaque tournoi
qu’il va jouer pour se classer, il doit affronter au moins 3 joueurs classés et il doit marquer au moins un point lors du premier tournoi.
Dès qu’il a joué suffisamment de tournois pour dépasser 9 parties, son premier classement est publié, si toutefois celui-ci dépasse 1 000
(seuil plancher au 1er juillet 2012). Ce premier classement est déterminé comme suit :
27 / 33
1. On calcule le « classement moyen » C
tournoi des tournois utilisés pour se classer.
Le calcul dépend du type de tournoi joué, tournoi toutes rondes ou système suisse (voir «
différents types de tournois » p.32-33).
Dans des tournois à système suisse ou par équipe, C
tournoi est tout simplement la moyenne des classements des adversaires classés.
Dans des tournois toutes rondes, les résultats des joueurs classés et non classés sont pris en compte. Pour les joueurs non classés,
C
tournoi est calculé comme suit :
- On calcule le classement moyen \(C_m\) des joueurs classés.
- On calcule la probabilité de gain \(p\) pour chacun des joueurs classés contre tous leurs adversaires :
On calcule ensuite \(D(p)\) pour chacun de ces joueurs.
On calcule la moyenne \(Dm\) de ces \(D(p)\).
- Alors Ctournoi \( = C_m - D_m \times \large \frac{n}{n\, +\, 1} \), où \(n\) est le nombre total d’adversaires des différents tournois.
28 / 33
2. On calcule comme plus haut la proportion \(p\) de points obtenus par le joueur contre ses adversaires :
$$p = \frac{\text{nombre de points obtenus}}{\text{nombre de parties disputées }}$$
On calcule alors \(D(p)\).
3. Pour obtenir le premier classement \(C\) du joueur :
Si \(p = 0,5\), alors \(C =\) C
tournoi
Si \(p > 0,5\), alors
\(C =\) C
tournoi + 15 × (nombre de demi-points obtenus au-dessus de la moitié des points),
c'est-à-dire \(C =\) C
tournoi + 15 \(\times \) (Nombre de victoires \(-\) Nombre de défaites).
Si \(p < 0,5\), alors \(C = \) C
tournoi \(+ D(p)\) pour un système suisse
\(C = \) C
tournoi \(+ D(p) \times \large \frac{n}{n\,+ \,1}\) pour un tournoi toutes rondes.
29 / 33
Exemple
Un joueur non classé a joué en système suisse 3 parties dans un tournoi contre des joueurs classés avec un classement moyen de 2 220,
un score de 1 sur 3, puis dans un autre tournoi 5 parties contre des joueurs classés avec une moyenne de 2 150, un score de 3 sur 5, et
ensuite dans un troisième tournoi 4 parties contre des joueurs classés avec une moyenne de 2 200, un score de 2,5 sur 4.
Le joueur a donc jouer 12 parties contre des joueurs classés donc au moins 9 parties, a marqué au moins un point et il avait au moins 3
joueurs classés dans chaque tournoi.
Le classement initial du joueur est calculé comme s’il avait joué 12 parties avec un score de 6,5 sur 12.
30 / 33
La moyenne de tous les adversaires est \(\large \frac{3\times 2\, 220 + 5\times 2\, 150 + 4\times 2\, 200}{12}\) \(\approx 2\, 184\)
Le joueur a obtenu un demi-point au-dessus de la moitié des points.
Le premier classement publié du nouveau joueur est \(2\, 184 + 15 = 2\, 199\).
Si ce joueur avait obtenu un score de 4,5 sur 12 sur les mêmes tournois, son premier classement serait :
$$\frac{3\times 2\,220 + 5\times 2\, 150 + 4\times 2\, 200 \;\;\;}{12} + D \left( \frac{4,5}{2} \right) \approx 2\, 095$$
31 / 33
Tournoi toutes rondes
Dans un tournoi d’échec, un tour est appelée une ronde.
Un tournoi (ou championnat) toutes rondes est un type de tournoi dans lequel les participants se rencontrent tous un nombre égal de
fois. Dans un tournoi toutes rondes simple, tous les participants sont opposés une seule fois au cours de la compétition.
Par exemple, la phases qualificative de la coupe du monde de football se déroule en toutes rondes.
Soit \(n\) le nombre de compétiteurs, le nombre de parties dans un tournoi toutes rondes simple sera de \(\large \frac{n(n-1)}{2} \)
(voir devoir en temps libre de terminale S «
Nouvel an »).
Si \(n\) est pair, il y aura \(n - 1\) rondes de \(\large \frac{n}{2}\) parties chacune, ces parties pouvant être organisées en parallèle. Si \(n\)
est impair, on ajoute un joueur fictif et son adversaire désigné ne joue pas.
32 / 33
Système suisse
Le système suisse ou système de tournoi suisse est un type de tournoi où les joueurs ou les équipes doivent s’affronter deux à deux. Il
s'agit d’une méthode permettant d'organiser des tournois regroupant un grand nombre de joueurs en un nombre réduit de confrontations.
Le premier tour est déterminé soit par tirage au sort, soit par têtes de série déterminées par leur classement.
Les joueurs qui gagnent reçoivent un point, ceux qui font match nul reçoivent un demi-point et les perdants ne reçoivent aucun point. Qu'ils
gagnent, perdent ou fassent match nul, tous les joueurs poursuivent le tournoi au tour suivant où les gagnants seront opposés aux gagnants,
les perdants aux perdants et ainsi de suite.
Au cours des tours suivants, les joueurs affrontent des adversaires qui comptent le même nombre de points (ou à peu près). Au cours d'un même
tournoi, aucun joueur ne rencontre deux fois le même adversaire. Aux échecs, on veille à ce que chaque joueur dispute le même nombre de parties
avec les blancs ou les noirs, si possible en alternance et tout au plus deux parties d'affilée avec la même couleur.
33 / 33



