\(V_{boule}=A_{sphère}\times\frac{R}{3}\)
3.b. En déduire, sur la fiche réponse, l'aire de la sphère de rayon \(R\).
20 / 21
3.a. Rappeler le volume d'une boule de rayon \(R\).
Ce volume fût aussi déterminé par Archimède en comparant les volumes d'une boule, d'un cylindre et d'un cône (sablier) de même hauteur.
19 / 21
Si on considère des géodes avec un nombre de faces de plus en plus grand (géode « 10 », géode « 100 », géode « 1 000 », géode « 10 000 » ... par exemple), la hauteur \(h\) de la géode se rapproche du rayon \(R\) de la sphère circonscrite, \(V_{géode}\) se rapproche de \(V_{boule}\) et \(A_{géode}\) se rapproche de \(A_{sphère}\).
De là, on trouve que
$$V_{boule}=A_{sphère}\times\frac{R}{3}$$
18 / 21
Rappel :
- \(V_{pyramide}=\large\frac{B\times h}{3}\).
- \(V_{géode}=n\times \large\frac{B\times h}{3}\).
Sur la fiche réponse, montrer que $$V_{géode}=A_{géode}\times\frac{h}{3}$$
17 / 21
Rappel :
- \(V_{géode}\) est le volume de la géode.
- \(V_{pyramide}\) le volume d'une des \(n\) pyramides identiques, \(h\) sa hauteur et \(B\) l'aire de sa base triangulaire.
- \(V_{pyramide}=\large\frac{B\times h}{3}\).
1.b. On peut en déduire que \(V_{géode}\) = ...
16 / 21
- Appelons \(V_{géode}\) le volume de la géode et \(A_{géode}\) son aire.
- Appelons \(V_{pyramide}\) le volume d'une des \(n\) pyramides identiques, \(h\) sa hauteur et \(B\) l'aire de sa base triangulaire.
- Appelons \(V_{boule}\) le volume de la boule circonscrite à la géode, \(A_{sphère}\) l'aire de la sphère circonscrite (la surface de la boule) et \(R\) son rayon.
1.a. \(V_{pyramide}\) = ...
15 / 21
- Appelons \(V_{géode}\) le volume de la géode et \(A_{géode}\) son aire.
- Appelons \(V_{pyramide}\) le volume d'une des \(n\) pyramides identiques, \(h\) sa hauteur et \(B\) l'aire de sa base triangulaire.
- Appelons \(V_{boule}\) le volume de la boule circonscrite à la géode, \(A_{sphère}\) l'aire de la sphère circonscrite (la surface de la boule) et \(R\) son rayon.
14 / 21
Géode et aire de la sphère
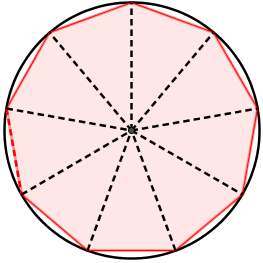
À la manière d'Archimède qui a approximé l'aire d'un disque par l'aire de polygones réguliers inscrits dans ce cercle, on va approximer le volume de la boule et l'aire de la sphère par ceux de géodes inscrites dans cette sphère.
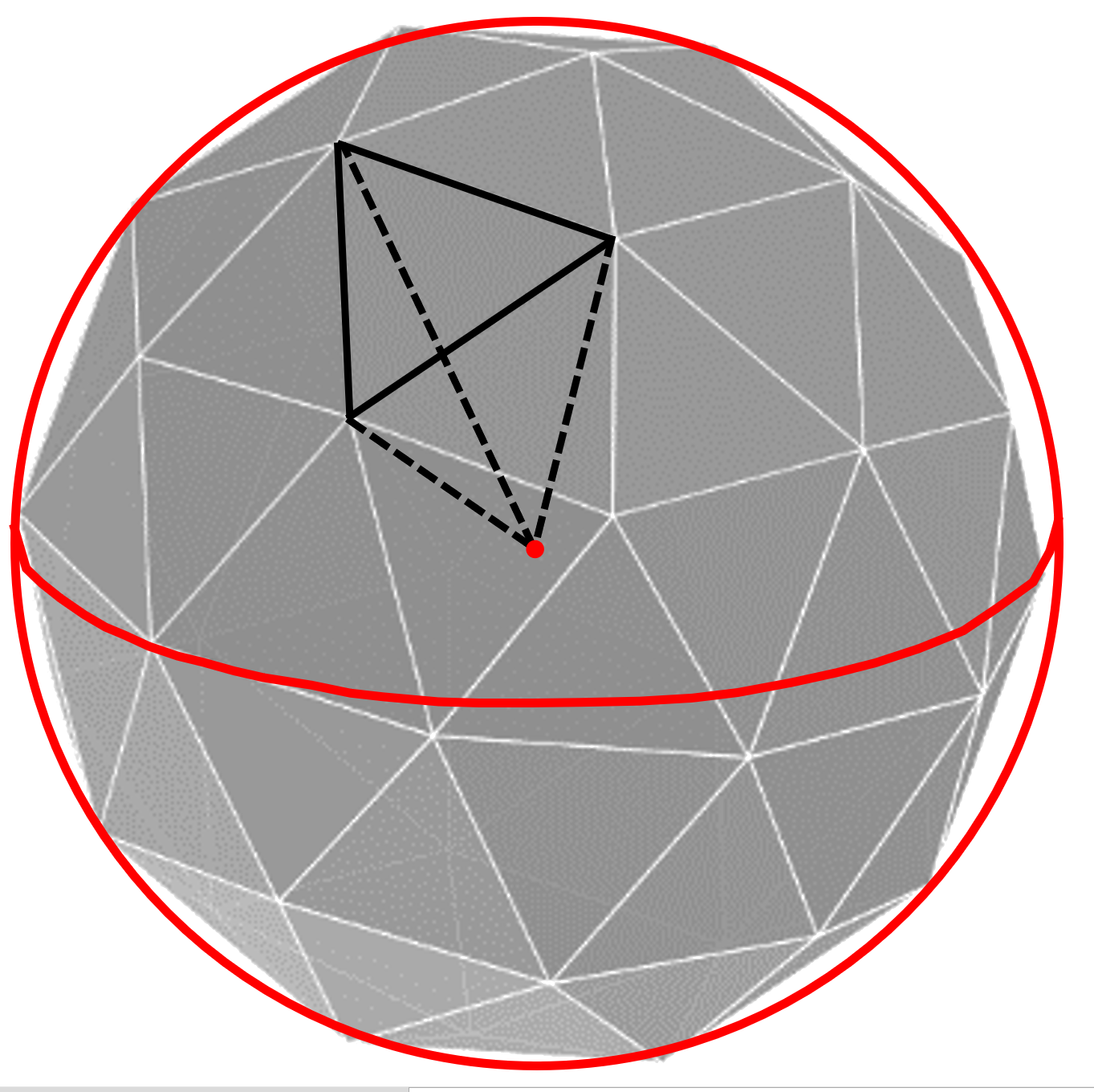
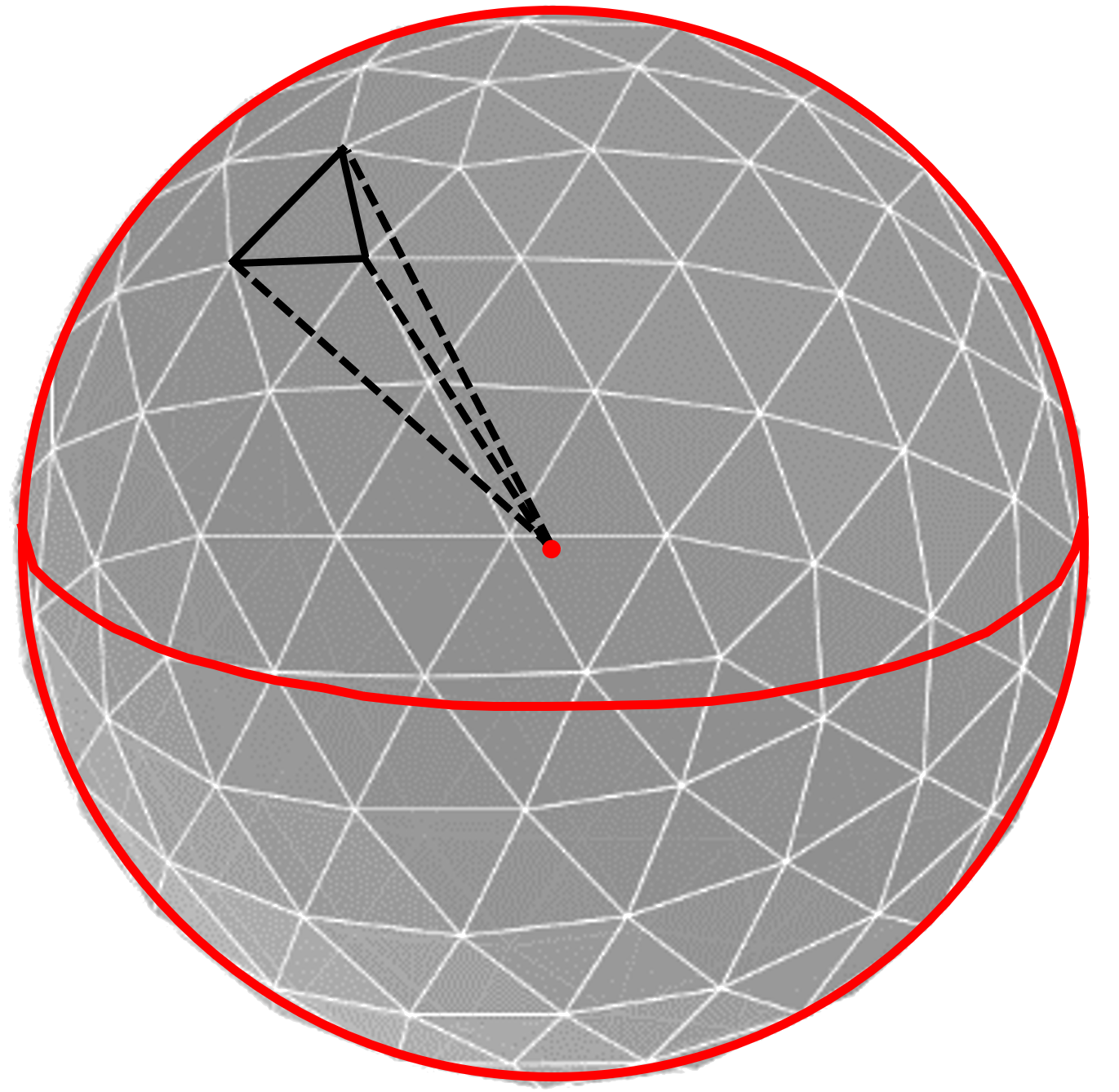
Une géode peut être vue comme composée de pyramides identiques dont chacune a pour base une face triangulaire de la géode et a pour sommet le centre de la géode (ou de la sphère circonscrite).
S'il y a \(n\) pyramides, le volume d'une géode est donc la somme des volumes de ces \(n\) pyramides identiques.
13 / 21
10. Rechercher sur Internet des exemples de structures (fabriquées ou naturelles) qui ont la forme d'une géode (normale ou duale).
Inscrire les exemples trouvés sur la fiche réponse.
12 / 21
9. Sur l'image de la Géode, retrouver un des sommets de l'icosaèdre initial.
Marquer ce sommet directement sur la fiche réponse.
11 / 21
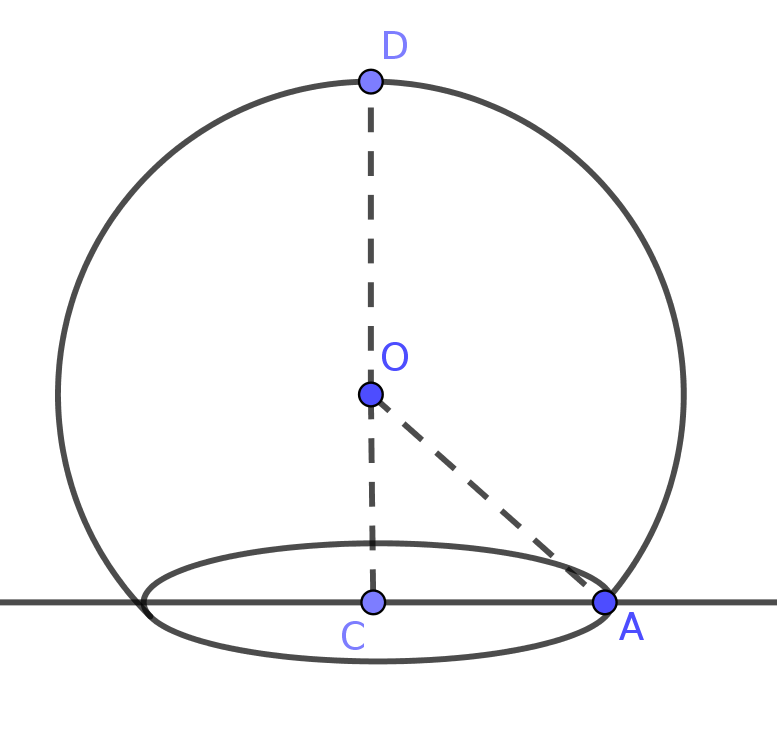8. La Géode de Paris a la forme d'une calotte sphérique. Le diamètre de la sphère est de 36 m et le diamètre de la surface au sol est de 29 m environ.
On souhaite calculer la hauteur de la Géode.
10 / 21
La Géode
Niveau : cycle 4.
Lien avec le programme : développer sa vision de l'espace. Utiliser un logiciel de géométrie pour visualiser des solides. Formule donnant le volume d'une pyramide, d'une boule. Représenter l'espace. Utiliser les notions de géométrie plane pour démontrer.
Lien avec Les maths au quotidien : Bâtiment, Solides de Platon.
Veuillez télécharger et imprimer la fiche réponse de cette activité en cliquant sur ce logo :
1 / 21
La Géode
La Géode est un bâtiment situé dans le parc de la Villette, dans le 19
e arrondissement de Paris. Elle accueille une salle de cinéma.
Elle fut inaugurée le 6 mai 1985 par François Mitterrand.
Bien que La Géode ait ouvert ses portes une année avant la Cité des sciences et de l'industrie, elle lui est aujourd'hui rattachée.
La Géode a la forme d'une géode (coupée), au sens géométrique.
La plupart des géodes sont construites à partir d'un polyèdre régulier qui s'appelle un icosaèdre.
2 / 21
1. Ouvrir l'applet Java "
polyLab "
(1).
Choisir un icosaèdre. Adapter l'échelle.
Combien ce polyèdre a-t-il de faces ?
(On pourra faire tourner le solide et choisir un des styles dans l'onglet "Attribut")
(1)L'applet Java polyLab.jar a été créée par
Jean-Bernard Roux.
3 / 21
2. Ce polyèdre admet-il une sphère circonscrite, c'est-à-dire une sphère passant par tous ses sommets ?
4 / 21
3. Visualiser une face de l'icosaèdre.
Quelle est la forme de cette face ?
5 / 21
Pour les trois questions suivantes, on rédigera la réponse sur la fiche réponse, que l'on remettra à son professeur à la fin de l'activité (ou à envoyer via le site Maths-au-quotidien.fr pour un amateur isolé).
4. Dans l'onglet « Généraux », choisir « Géode » (et remarquer le nombre « 2 » par défaut).
Passer de l'icosaèdre à la géode un certain nombre de fois.
Expliquer comment est construite cette géode à partir de l'icosaèdre.
6 / 21
5. Dans le choix « Géode », modifier le nombre « 2 » et choisir « 3 ».
Expliquer, sur la fiche réponse, comment est construite cette nouvelle géode à partir de l'icosaèdre.
7 / 21
6. Pour les géodes « 2 » et « 3 », choisir « polyèdre dual » dans l'onglet « Opérations ».
On obtient les géodes duales.
Comment sont-elles construites à partir des deux premières ?
8 / 21
7. La Géode de Paris est une géode (coupée) où le nombre choisi est « 10 ».
Visualiser la géode « 10 ».
Compléter la phrase suivante :
9 / 21
Vous avez obtenu un taux de réussite de :
- Fin -
21 / 21
