Sillage

Niveau : Terminale générale.

Lien avec le programme : document annexe "Va-t-on faire des vagues". Ouverture interdisciplinaire.
En mathématiques : Calculer la dérivée de \(x\mapsto\sqrt{u(x)}\).
En physique : ondes dans la matière, extraire et exploiter des informations sur les manifestations des ondes mécaniques dans la matière. Ondes progressives périodiques, distances et vitesse de propagation. Pour une onde progressive sinusoïdale, période, fréquence et longueur d'onde.
Lien avec Les maths au quotidien : Transport.

Dans l'activité Mur du son, nous avons mis en évidence le cône de Mach d'un avion voyageant à vitesse supersonique.

Si l'on coupe ce cône par le plan des ailes de l'avion, nous obtenons un secteur angulaire, dont le sinus de l'angle \(\alpha\) est inversement proportionnel à la vitesse \(V\) de l'avion par la relation \(sin (\alpha) = \frac{1}{nombre\,de\,Mach}\), c'est-à-dire \(sin (\alpha) = \frac{Vitesse\,du\,son}{Vitesse\,de\,l'avion}\).

Par conséquent, plus l'avion est rapide, plus l'angle au sommet du cône est petit.

Intéressons-nous à présent au sillage laissé sur l'eau par un canard ou un bateau. Il a, vous l'aviez remarqué, également la forme d'un secteur angulaire, c'est-à-dire la forme d'un "V". Ce qui vous a peut-être échappé, c'est que contrairement à l'avion, l'angle au sommet de ce secteur angulaire ne varie pas suivant la vitesse ou la taille du mobile qui laisse ce sillage. Cet angle vaut universellement 39° environ.

Enfin ceci est vrai si l'eau est suffisamment profonde, et si la vitesse est suffisante pour créer un sillage.

C'est au XIXe siècle (1887) que William Thomson, alias Lord Kelvin (oui, l'homme des thermomètres...), fut le premier à expliquer la forme du sillage.
Nous allons tâcher d'illustrer géométriquement ce phénomène.

La physique nous indique que lorsque le bateau se déplace, il crée une perturbation de la surface de l'eau qui se propage : des ondes dites élémentaires se déplacent à la surface de l'eau, ce sont des petites vaguelettes presque imperceptibles.

Ces ondes élémentaires ont des vitesses différentes, et elles se décalent les unes par rapport aux autres au cours du temps, et construisent une vague plus grosse (les hauteurs de toutes les petites vaguelettes se sont ajoutées de manière maximale).

La physique montre qu'en eau profonde, et pourvu que le bateau ne soit pas non plus excessivement rapide, la vitesse de propagation de la vague dans une certaine direction est égale à la moitié de la vitesse moyenne des ondes élémentaires.

Pour les terminales générales, un exercice ICI

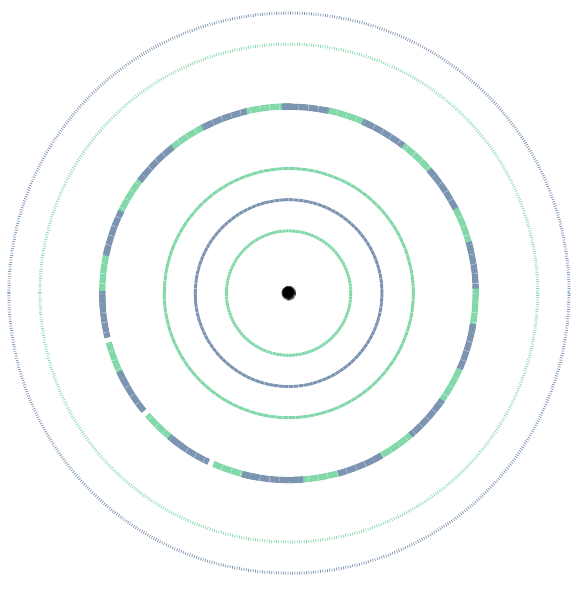
C'est comme quand on jette un caillou dans l'eau : il se forme une multitude de vaguelettes presque imperceptibles qui partent en cercles. Voici un exemple avec deux ondes dont on visualise les crêtes à différents instants. Leurs amplitudes s'ajoutent au niveau du "gros" cercle en pointillés (vague) qui avance deux fois moins vite qu'elles en moyenne, et elle disparaissent au-delà de cette vague.

Voici une petite vidéo où l'on voit une goutte tomber dans l'eau et générer des ondes élémentaires dans toutes les directions. On voit bien les ondes élémentaires doubler la "vague" (deux fois plus vite) : ICI

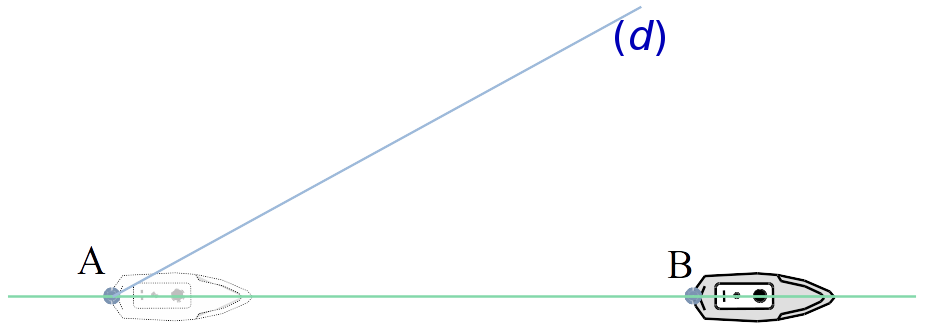
D'autre part, prenons un bateau émettant en A une onde élémentaire qui part en ligne droite dans une certaine direction.



Lorsque le bateau arrive au point B, la physique montre qu'elle se retrouve en F telle que (AF) est perpendiculaire à (FB) (l'aspect de la déformation de la surface de l'eau par l'onde ne change pas, on dit que l'onde est stationnaire). On appelle G le point de la vague sur cette droite. On rappelle que la vague voyage deux fois moins vite que les ondes élémentaires.

Il est temps de tirer toutes les conclusions mathématiques de ces résultats :

Dans une feuille GeoGebra :

- représenter les points A et B suivant le modèle ci-contre
- tracer la droite (AB) et la demi-droite (\(d\))
- construire le point F
- construire le point G
- faire varier la direction de la demi-droite (\(d\))

L'ensemble du front d'ondes élémentaires émises en A, lorsque le bateau est en B, est :

le de [AB].

Remarque : on dit aussi que la vague est le front de groupe, car c'est un "paquet" d'ondes d'énergie maximale.


Lorsque le bateau se déplace du point A au point B, il a créé en chaque point de sa trajectoire une vague (cercle du front de groupe).
Voici deux fichiers GeoGebra où l'on voit l'ensemble de ces cercles :

Le sillage est le secteur angulaire délimité par les deux tangentes à tous ces cercles (à rapprocher du cône de Mach).
On observe déjà que l'angle de ce secteur angulaire ne dépend pas des caractéristiques du bateau...

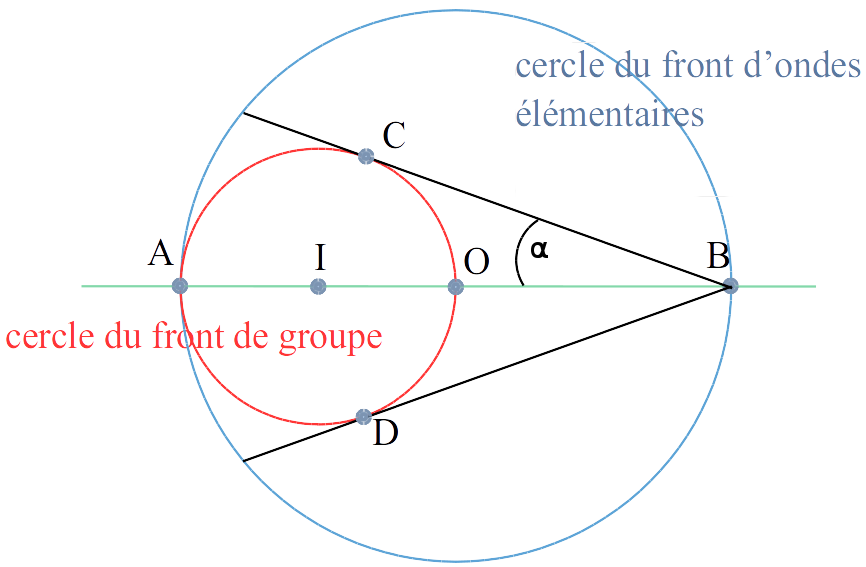
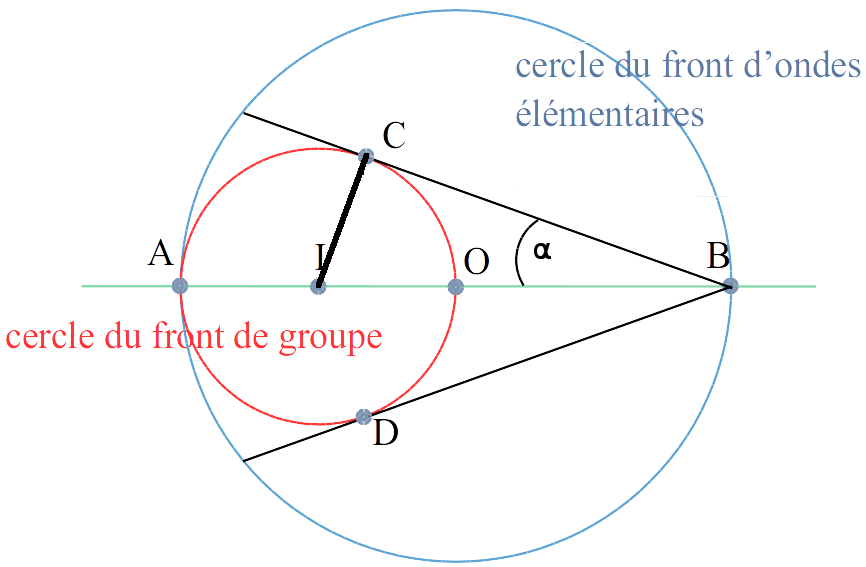
Détermination de l'angle \(\alpha\) du sillage de Kelvin

On rappelle que AB = 2AO et que les droites (BC) et (BD) sont tangentes au cercle de diamètre [AO].
Soit I le centre de ce cercle.

Le triangle ICB est en

\(sin (\alpha) = \) (entrer une fraction)


\( \alpha \approx \) ° (arrondir à 2 décimales)

On sait maintenant que \(\alpha \approx 19,47^o\),

On en déduit l'angle au sommet du sillage :

° (arrondir à deux décimales)

Nous avons vu que le rayon du cercle du front d'ondes élémentaires généré au point A par le bateau mobile augmente avec le temps tandis que ce cercle se déplace, en quelque sorte entrainé par le mouvement du bateau.
Si le bateau avance à une vitesse V, alors :

- les cercles du front d'ondes élémentaires émis à chaque instant grossissent à une vitesse de
- le centre de chacun de ces cercles se déplace à une vitesse de

Nous avons vu que le rayon du cercle du front d'ondes élémentaires généré au point A par le bateau mobile augmente avec le temps tandis que ce cercle se déplace, en quelque sorte entrainé par le mouvement du bateau.
Si le bateau avance à une vitesse V, alors :

- les cercles du front de groupe émis à chaque instant grossissent à une vitesse de
- le centre de chacun de ces cercles se déplace à une vitesse de



Remarque : les sphères du cône de Mach grossissent à la vitesse du son et leurs centres ne se déplacent pas.

Pour finir...

Depuis le début des années 2010, (eh oui, c'est très récent), on sait que le résultat précédent n'est vrai qu'en dessous d'une vitesse critique, à partir de laquelle le sillage va bel et bien se rétrécir, et de manière inversement proportionnellement à la vitesse, exactement comme le cône de Mach dans le cas d'un avion !!!

Cette vitesse critique dépend de la longueur du mobile qui vogue. Elle est de l'ordre de la vitesse de déjaugeage (le bateau est "porté" par la surface de l'eau).

Vous avez obtenu un taux de réussite de :

- Fin -