Le problème de Steiner dans un triangle

Niveau : cycle 4

Lien avec le programme : triangle, somme des angles, inégalité triangulaire, cas d’égalité des triangles. Mettre en œuvre ou écrire un protocole de construction d’une figure géométrique. Comprendre l’effet d’une rotation sur une figure. Utiliser un logiciel de géométrie dynamique. Résoudre des problèmes de géométrie plane, prouver un résultat général, valider ou réfuter une conjecture. Caractérisation du triangle équilatéral, alignement de points, angles (cycle 3).

Lien avec Les Maths au quotidien : représentations visuelles, transport.

Première situation

On considère deux plaques parallèles en plexiglas, reliées par trois bâtonnets perpendiculairement. On trempe ce dispositif dans de l’eau savonneuse, on la sort délicatement et on regarde ce qui se passe. Un film de savon s’est formé, reliant les trois bâtonnets. Ce film, composé de trois rectangles, est perpendiculaire à la surface desplaques (loi de Plateau). Vu de dessus, les bâtonnets forment un triangle et le film trois segments reliant les sommets à un point singulier, intérieur au triangle. L’aire du film de savon est la somme de celles des trois rectangles de même largeur (l’écartement entre les plaques) et dont les longueurs sont les distances du point singulier aux sommets du triangle.
La physique nous indique que le film de savon minimise son aire (énergie potentielle minimale). La somme des trois distances est également minimisée...

Deuxième situation

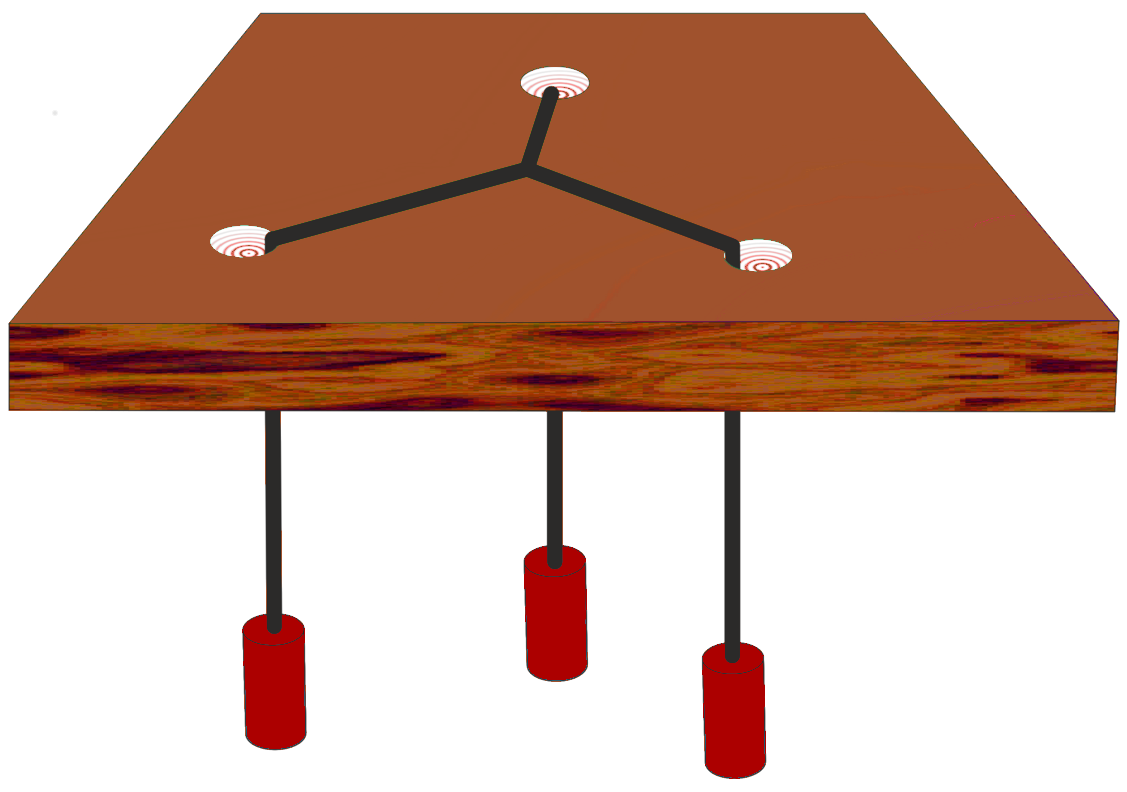
On perce trois trous sur une plaque de bois suivant un triangle. On fait passer par les trous trois ficelles à l'extrémité desquelles on suspend des poids de masse identique. On réunit ces ficelles par un nœud. Quand le système est en équilibre, son énergie potentielleest minimale : la somme des trois altitudes des trois poids est minimale. Cela se produit quand la somme des longueurs verticales des trois ficelles est maximale, c'est-à-dire quand la somme des longueurs horizontales des trois ficelles est minimale...

Soit ABC un triangle dont tous les angles sont inférieurs à 120°. On admet qu’il existe un point et un seul, noté F, à l’intérieur du triangle ABC, tel que la somme des longueurs AF + BF + CF soit minimale.

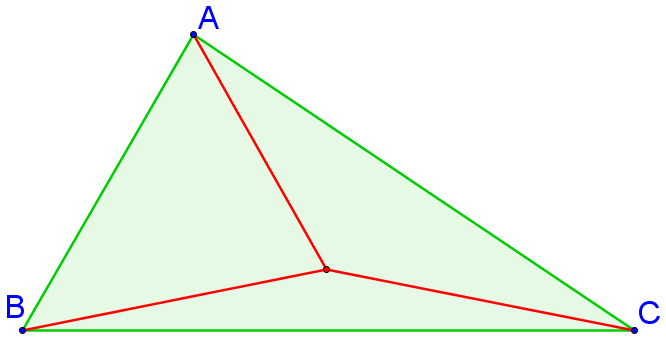
Ce point est appelé point de Fermat du triangle ABC
(ou point de Torricelli, ou point de Steiner).

Ci-contre, un point à l’intérieur du triangle (qui n’est pas F...)

Ouvrir les deux fichiers GeoGebra ci-contre et émettre pour chaque situation une conjecture.


Écrire une conjecture n°1 ici.


Écrire une conjecture n°2 ici.

Démonstrations des conjectures

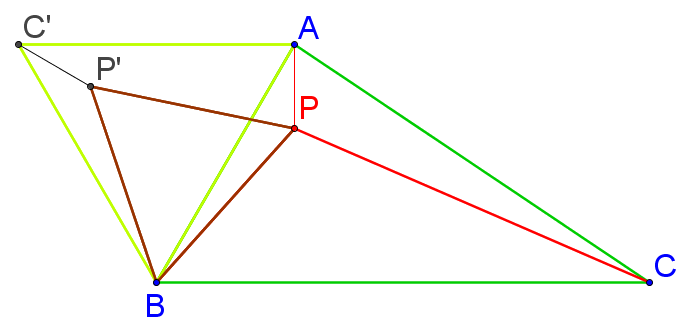
Supposons qu’aucun angle du triangle ABC n’est supérieur à 120°.
On construit sur [AB] le triangle équilatéral BAC’.
Soit P un point à l’intérieur du triangle ABC.
On considère alors l’image du triangle ABP par la rotation de centre B et d’angle 60° (sens direct : inverse des aiguilles d’une montre).

La figure obtenue est un , qui est au triangle ABP.
Le point est commun aux deux triangles. L’image de A est . On note P’ l’image de P par cette rotation.