Démonstrations des conjectures
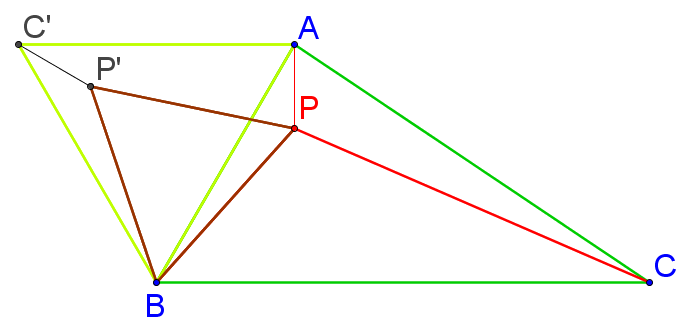 Supposons qu’aucun angle du triangle ABC n’est supérieur à 120°.
Supposons qu’aucun angle du triangle ABC n’est supérieur à 120°.
On construit sur [AB] le triangle équilatéral BAC’.
Soit P un point à l’intérieur du triangle ABC.
On considère alors l’image du triangle ABP par la rotation de centre B et d’angle 60° (sens direct : inverse des aiguilles d’une montre).
6 / 17
 Supposons qu’aucun angle du triangle ABC n’est supérieur à 120°.
Supposons qu’aucun angle du triangle ABC n’est supérieur à 120°.